Neural Networks

Neural networks can be constructed using the torch.nn package.

Now that you had a glimpse of autograd, nn depends on autograd to define models and differentiate them. An nn.Module contains layers, and a method forward(input) that returns the output.

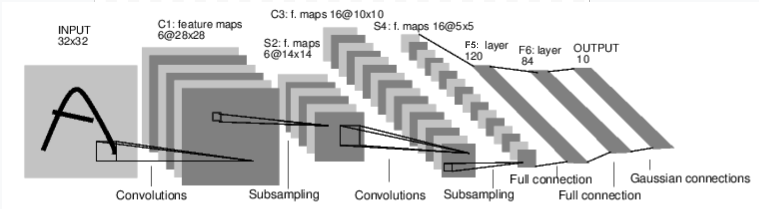
For example, look at this network that classifies digit images:

convnet

It is a simple feed-forward network. It takes the input, feeds it through several layers one after the other, and then finally gives the output.

A typical training procedure for a neural network is as follows:

• Define the neural network that has some learnable parameters (or weights)

• Iterate over a dataset of inputs

• Process input through the network

• Compute the loss (how far is the output from being correct)

• Propagate gradients back into the network’s parameters

• Update the weights of the network, typically using a simple update rule: weight = weight - learning_rate * gradient

Define the network

Let’s define this network:

import torch
import torch.nn as nn
import torch.nn.functional as F


class Net(nn.Module):

    def __init__(self):
        super(Net, self).__init__()
        # 1 input image channel, 6 output channels, 5x5 square convolution
        # kernel
        self.conv1 = nn.Conv2d(1, 6, 5)
        self.conv2 = nn.Conv2d(6, 16, 5)
        # an affine operation: y = Wx + b
        self.fc1 = nn.Linear(16 * 5 * 5, 120)  # 5*5 from image dimension
        self.fc2 = nn.Linear(120, 84)
        self.fc3 = nn.Linear(84, 10)

    def forward(self, input):
        # Convolution layer C1: 1 input image channel, 6 output channels,
        # 5x5 square convolution, it uses RELU activation function, and
        # outputs a Tensor with size (N, 6, 28, 28), where N is the size of the batch
        c1 = F.relu(self.conv1(input))
        # Subsampling layer S2: 2x2 grid, purely functional,
        # this layer does not have any parameter, and outputs a (N, 6, 14, 14) Tensor
        s2 = F.max_pool2d(c1, (2, 2))
        # Convolution layer C3: 6 input channels, 16 output channels,
        # 5x5 square convolution, it uses RELU activation function, and
        # outputs a (N, 16, 10, 10) Tensor
        c3 = F.relu(self.conv2(s2))
        # Subsampling layer S4: 2x2 grid, purely functional,
        # this layer does not have any parameter, and outputs a (N, 16, 5, 5) Tensor
        s4 = F.max_pool2d(c3, 2)
        # Flatten operation: purely functional, outputs a (N, 400) Tensor
        s4 = torch.flatten(s4, 1)
        # Fully connected layer F5: (N, 400) Tensor input,
        # and outputs a (N, 120) Tensor, it uses RELU activation function
        f5 = F.relu(self.fc1(s4))
        # Fully connected layer F6: (N, 120) Tensor input,
        # and outputs a (N, 84) Tensor, it uses RELU activation function
        f6 = F.relu(self.fc2(f5))
        # Gaussian layer OUTPUT: (N, 84) Tensor input, and
        # outputs a (N, 10) Tensor
        output = self.fc3(f6)
        return output


net = Net()
print(net)

Net(
  (conv1): Conv2d(1, 6, kernel_size=(5, 5), stride=(1, 1))
  (conv2): Conv2d(6, 16, kernel_size=(5, 5), stride=(1, 1))
  (fc1): Linear(in_features=400, out_features=120, bias=True)
  (fc2): Linear(in_features=120, out_features=84, bias=True)
  (fc3): Linear(in_features=84, out_features=10, bias=True)
)

You just have to define the forward function, and the backward function (where gradients are computed) is automatically defined for you using autograd. You can use any of the Tensor operations in the forward function.

The learnable parameters of a model are returned by net.parameters()

params = list(net.parameters())
print(len(params))
print(params[0].size())  # conv1's .weight

10
torch.Size([6, 1, 5, 5])

Let’s try a random 32x32 input. Note: expected input size of this net (LeNet) is 32x32. To use this net on the MNIST dataset, please resize the images from the dataset to 32x32.

input = torch.randn(1, 1, 32, 32)
out = net(input)
print(out)

tensor([[ 0.1453, -0.0590, -0.0065,  0.0905,  0.0146, -0.0805, -0.1211, -0.0394,
         -0.0181, -0.0136]], grad_fn=<AddmmBackward0>)

Zero the gradient buffers of all parameters and backprops with random gradients:

net.zero_grad()
out.backward(torch.randn(1, 10))

Note

torch.nn only supports mini-batches. The entire torch.nn package only supports inputs that are a mini-batch of samples, and not a single sample.

For example, nn.Conv2d will take in a 4D Tensor of nSamples x nChannels x Height x Width.

If you have a single sample, just use input.unsqueeze(0) to add a fake batch dimension.

Before proceeding further, let’s recap all the classes you’ve seen so far.

Recap:

• torch.Tensor - A multi-dimensional array with support for autograd operations like backward(). Also holds the gradient w.r.t. the tensor.

• nn.Module - Neural network module. Convenient way of encapsulating parameters, with helpers for moving them to GPU, exporting, loading, etc.

• nn.Parameter - A kind of Tensor, that is automatically registered as a parameter when assigned as an attribute to a Module.

• autograd.Function - Implements forward and backward definitions of an autograd operation. Every Tensor operation creates at least a single Function node that connects to functions that created a Tensor and encodes its history.

At this point, we covered:

• Defining a neural network

• Processing inputs and calling backward

Still Left:

• Computing the loss

• Updating the weights of the network

Loss Function

A loss function takes the (output, target) pair of inputs, and computes a value that estimates how far away the output is from the target.

There are several different loss functions under the nn package . A simple loss is: nn.MSELoss which computes the mean-squared error between the output and the target.

For example:

output = net(input)
target = torch.randn(10)  # a dummy target, for example
target = target.view(1, -1)  # make it the same shape as output
criterion = nn.MSELoss()

loss = criterion(output, target)
print(loss)

tensor(1.3619, grad_fn=<MseLossBackward0>)

Now, if you follow loss in the backward direction, using its .grad_fn attribute, you will see a graph of computations that looks like this:

input -> conv2d -> relu -> maxpool2d -> conv2d -> relu -> maxpool2d
      -> flatten -> linear -> relu -> linear -> relu -> linear
      -> MSELoss
      -> loss

So, when we call loss.backward(), the whole graph is differentiated w.r.t. the neural net parameters, and all Tensors in the graph that have requires_grad=True will have their .grad Tensor accumulated with the gradient.

For illustration, let us follow a few steps backward:

print(loss.grad_fn)  # MSELoss
print(loss.grad_fn.next_functions[0][0])  # Linear
print(loss.grad_fn.next_functions[0][0].next_functions[0][0])  # ReLU

<MseLossBackward0 object at 0x7f904d617730>
<AddmmBackward0 object at 0x7f904d614220>
<AccumulateGrad object at 0x7f904d614b20>

Backprop

To backpropagate the error all we have to do is to loss.backward(). You need to clear the existing gradients though, else gradients will be accumulated to existing gradients.

Now we shall call loss.backward(), and have a look at conv1’s bias gradients before and after the backward.

net.zero_grad()     # zeroes the gradient buffers of all parameters

print('conv1.bias.grad before backward')
print(net.conv1.bias.grad)

loss.backward()

print('conv1.bias.grad after backward')
print(net.conv1.bias.grad)

conv1.bias.grad before backward
None
conv1.bias.grad after backward
tensor([ 0.0081, -0.0080, -0.0039,  0.0150,  0.0003, -0.0105])

Now, we have seen how to use loss functions.

Read Later:

The neural network package contains various modules and loss functions that form the building blocks of deep neural networks. A full list with documentation is here.

The only thing left to learn is:

• Updating the weights of the network

Update the weights

The simplest update rule used in practice is the Stochastic Gradient Descent (SGD):

weight = weight - learning_rate * gradient

We can implement this using simple Python code:

learning_rate = 0.01
for f in net.parameters():
    f.data.sub_(f.grad.data * learning_rate)

However, as you use neural networks, you want to use various different update rules such as SGD, Nesterov-SGD, Adam, RMSProp, etc. To enable this, we built a small package: torch.optim that implements all these methods. Using it is very simple:

import torch.optim as optim

# create your optimizer
optimizer = optim.SGD(net.parameters(), lr=0.01)

# in your training loop:
optimizer.zero_grad()   # zero the gradient buffers
output = net(input)
loss = criterion(output, target)
loss.backward()
optimizer.step()    # Does the update

Note

Observe how gradient buffers had to be manually set to zero using optimizer.zero_grad(). This is because gradients are accumulated as explained in the Backprop section.