Introduction || Tensors || Autograd || Building Models || TensorBoard Support || Training Models || Model Understanding

Introduction to PyTorch

Created On: Nov 30, 2021 | Last Updated: Jan 19, 2024 | Last Verified: Nov 05, 2024

Follow along with the video below or on youtube.

PyTorch Tensors

Follow along with the video beginning at 03:50.

First, we’ll import pytorch.

import torch

Let’s see a few basic tensor manipulations. First, just a few of the ways to create tensors:

z = torch.zeros(5, 3)
print(z)
print(z.dtype)

tensor([[0., 0., 0.],
        [0., 0., 0.],
        [0., 0., 0.],
        [0., 0., 0.],
        [0., 0., 0.]])
torch.float32

Above, we create a 5x3 matrix filled with zeros, and query its datatype to find out that the zeros are 32-bit floating point numbers, which is the default PyTorch.

What if you wanted integers instead? You can always override the default:

i = torch.ones((5, 3), dtype=torch.int16)
print(i)

tensor([[1, 1, 1],
        [1, 1, 1],
        [1, 1, 1],
        [1, 1, 1],
        [1, 1, 1]], dtype=torch.int16)

You can see that when we do change the default, the tensor helpfully reports this when printed.

It’s common to initialize learning weights randomly, often with a specific seed for the PRNG for reproducibility of results:

torch.manual_seed(1729)
r1 = torch.rand(2, 2)
print('A random tensor:')
print(r1)

r2 = torch.rand(2, 2)
print('\nA different random tensor:')
print(r2) # new values

torch.manual_seed(1729)
r3 = torch.rand(2, 2)
print('\nShould match r1:')
print(r3) # repeats values of r1 because of re-seed

A random tensor:
tensor([[0.3126, 0.3791],
        [0.3087, 0.0736]])

A different random tensor:
tensor([[0.4216, 0.0691],
        [0.2332, 0.4047]])

Should match r1:
tensor([[0.3126, 0.3791],
        [0.3087, 0.0736]])

PyTorch tensors perform arithmetic operations intuitively. Tensors of similar shapes may be added, multiplied, etc. Operations with scalars are distributed over the tensor:

ones = torch.ones(2, 3)
print(ones)

twos = torch.ones(2, 3) * 2 # every element is multiplied by 2
print(twos)

threes = ones + twos       # addition allowed because shapes are similar
print(threes)              # tensors are added element-wise
print(threes.shape)        # this has the same dimensions as input tensors

r1 = torch.rand(2, 3)
r2 = torch.rand(3, 2)
# uncomment this line to get a runtime error
# r3 = r1 + r2

tensor([[1., 1., 1.],
        [1., 1., 1.]])
tensor([[2., 2., 2.],
        [2., 2., 2.]])
tensor([[3., 3., 3.],
        [3., 3., 3.]])
torch.Size([2, 3])

Here’s a small sample of the mathematical operations available:

r = (torch.rand(2, 2) - 0.5) * 2 # values between -1 and 1
print('A random matrix, r:')
print(r)

# Common mathematical operations are supported:
print('\nAbsolute value of r:')
print(torch.abs(r))

# ...as are trigonometric functions:
print('\nInverse sine of r:')
print(torch.asin(r))

# ...and linear algebra operations like determinant and singular value decomposition
print('\nDeterminant of r:')
print(torch.det(r))
print('\nSingular value decomposition of r:')
print(torch.svd(r))

# ...and statistical and aggregate operations:
print('\nAverage and standard deviation of r:')
print(torch.std_mean(r))
print('\nMaximum value of r:')
print(torch.max(r))

A random matrix, r:
tensor([[ 0.9956, -0.2232],
        [ 0.3858, -0.6593]])

Absolute value of r:
tensor([[0.9956, 0.2232],
        [0.3858, 0.6593]])

Inverse sine of r:
tensor([[ 1.4775, -0.2251],
        [ 0.3961, -0.7199]])

Determinant of r:
tensor(-0.5703)

Singular value decomposition of r:
torch.return_types.svd(
U=tensor([[-0.8353, -0.5497],
        [-0.5497,  0.8353]]),
S=tensor([1.1793, 0.4836]),
V=tensor([[-0.8851, -0.4654],
        [ 0.4654, -0.8851]]))

Average and standard deviation of r:
(tensor(0.7217), tensor(0.1247))

Maximum value of r:
tensor(0.9956)

There’s a good deal more to know about the power of PyTorch tensors, including how to set them up for parallel computations on GPU - we’ll be going into more depth in another video.

PyTorch Models

Follow along with the video beginning at 10:00.

Let’s talk about how we can express models in PyTorch

import torch                     # for all things PyTorch
import torch.nn as nn            # for torch.nn.Module, the parent object for PyTorch models
import torch.nn.functional as F  # for the activation function

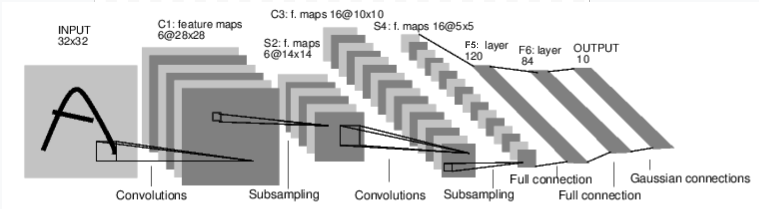
Figure: LeNet-5

Above is a diagram of LeNet-5, one of the earliest convolutional neural nets, and one of the drivers of the explosion in Deep Learning. It was built to read small images of handwritten numbers (the MNIST dataset), and correctly classify which digit was represented in the image.

Here’s the abridged version of how it works:

• Layer C1 is a convolutional layer, meaning that it scans the input image for features it learned during training. It outputs a map of where it saw each of its learned features in the image. This “activation map” is downsampled in layer S2.

• Layer C3 is another convolutional layer, this time scanning C1’s activation map for combinations of features. It also puts out an activation map describing the spatial locations of these feature combinations, which is downsampled in layer S4.

• Finally, the fully-connected layers at the end, F5, F6, and OUTPUT, are a classifier that takes the final activation map, and classifies it into one of ten bins representing the 10 digits.

How do we express this simple neural network in code?

class LeNet(nn.Module):

    def __init__(self):
        super(LeNet, self).__init__()
        # 1 input image channel (black & white), 6 output channels, 5x5 square convolution
        # kernel
        self.conv1 = nn.Conv2d(1, 6, 5)
        self.conv2 = nn.Conv2d(6, 16, 5)
        # an affine operation: y = Wx + b
        self.fc1 = nn.Linear(16 * 5 * 5, 120)  # 5*5 from image dimension
        self.fc2 = nn.Linear(120, 84)
        self.fc3 = nn.Linear(84, 10)

    def forward(self, x):
        # Max pooling over a (2, 2) window
        x = F.max_pool2d(F.relu(self.conv1(x)), (2, 2))
        # If the size is a square you can only specify a single number
        x = F.max_pool2d(F.relu(self.conv2(x)), 2)
        x = x.view(-1, self.num_flat_features(x))
        x = F.relu(self.fc1(x))
        x = F.relu(self.fc2(x))
        x = self.fc3(x)
        return x

    def num_flat_features(self, x):
        size = x.size()[1:]  # all dimensions except the batch dimension
        num_features = 1
        for s in size:
            num_features *= s
        return num_features

Looking over this code, you should be able to spot some structural similarities with the diagram above.

This demonstrates the structure of a typical PyTorch model:

• It inherits from torch.nn.Module - modules may be nested - in fact, even the Conv2d and Linear layer classes inherit from torch.nn.Module.

• A model will have an __init__() function, where it instantiates its layers, and loads any data artifacts it might need (e.g., an NLP model might load a vocabulary).

• A model will have a forward() function. This is where the actual computation happens: An input is passed through the network layers and various functions to generate an output.

• Other than that, you can build out your model class like any other Python class, adding whatever properties and methods you need to support your model’s computation.

Let’s instantiate this object and run a sample input through it.

net = LeNet()
print(net)                         # what does the object tell us about itself?

input = torch.rand(1, 1, 32, 32)   # stand-in for a 32x32 black & white image
print('\nImage batch shape:')
print(input.shape)

output = net(input)                # we don't call forward() directly
print('\nRaw output:')
print(output)
print(output.shape)

LeNet(
  (conv1): Conv2d(1, 6, kernel_size=(5, 5), stride=(1, 1))
  (conv2): Conv2d(6, 16, kernel_size=(5, 5), stride=(1, 1))
  (fc1): Linear(in_features=400, out_features=120, bias=True)
  (fc2): Linear(in_features=120, out_features=84, bias=True)
  (fc3): Linear(in_features=84, out_features=10, bias=True)
)

Image batch shape:
torch.Size([1, 1, 32, 32])

Raw output:
tensor([[ 0.0898,  0.0318,  0.1485,  0.0301, -0.0085, -0.1135, -0.0296,  0.0164,
          0.0039,  0.0616]], grad_fn=<AddmmBackward0>)
torch.Size([1, 10])

There are a few important things happening above:

First, we instantiate the LeNet class, and we print the net object. A subclass of torch.nn.Module will report the layers it has created and their shapes and parameters. This can provide a handy overview of a model if you want to get the gist of its processing.

Below that, we create a dummy input representing a 32x32 image with 1 color channel. Normally, you would load an image tile and convert it to a tensor of this shape.

You may have noticed an extra dimension to our tensor - the batch dimension. PyTorch models assume they are working on batches of data - for example, a batch of 16 of our image tiles would have the shape (16, 1, 32, 32). Since we’re only using one image, we create a batch of 1 with shape (1, 1, 32, 32).

We ask the model for an inference by calling it like a function: net(input). The output of this call represents the model’s confidence that the input represents a particular digit. (Since this instance of the model hasn’t learned anything yet, we shouldn’t expect to see any signal in the output.) Looking at the shape of output, we can see that it also has a batch dimension, the size of which should always match the input batch dimension. If we had passed in an input batch of 16 instances, output would have a shape of (16, 10).

Datasets and Dataloaders

Follow along with the video beginning at 14:00.

Below, we’re going to demonstrate using one of the ready-to-download, open-access datasets from TorchVision, how to transform the images for consumption by your model, and how to use the DataLoader to feed batches of data to your model.

The first thing we need to do is transform our incoming images into a PyTorch tensor.

#%matplotlib inline

import torch
import torchvision
import torchvision.transforms as transforms

transform = transforms.Compose(
    [transforms.ToTensor(),
     transforms.Normalize((0.4914, 0.4822, 0.4465), (0.2470, 0.2435, 0.2616))])

Here, we specify two transformations for our input:

• transforms.ToTensor() converts images loaded by Pillow into PyTorch tensors.

• transforms.Normalize() adjusts the values of the tensor so that their average is zero and their standard deviation is 1.0. Most activation functions have their strongest gradients around x = 0, so centering our data there can speed learning. The values passed to the transform are the means (first tuple) and the standard deviations (second tuple) of the rgb values of the images in the dataset. You can calculate these values yourself by running these few lines of code:

  ```

  from torch.utils.data import ConcatDataset transform = transforms.Compose([transforms.ToTensor()]) trainset = torchvision.datasets.CIFAR10(root=’./data’, train=True,

  download=True, transform=transform)

  #stack all train images together into a tensor of shape #(50000, 3, 32, 32) x = torch.stack([sample[0] for sample in ConcatDataset([trainset])])

  #get the mean of each channel mean = torch.mean(x, dim=(0,2,3)) #tensor([0.4914, 0.4822, 0.4465]) std = torch.std(x, dim=(0,2,3)) #tensor([0.2470, 0.2435, 0.2616])

  ```

There are many more transforms available, including cropping, centering, rotation, and reflection.

Next, we’ll create an instance of the CIFAR10 dataset. This is a set of 32x32 color image tiles representing 10 classes of objects: 6 of animals (bird, cat, deer, dog, frog, horse) and 4 of vehicles (airplane, automobile, ship, truck):

trainset = torchvision.datasets.CIFAR10(root='./data', train=True,
                                        download=True, transform=transform)

Downloading https://www.cs.toronto.edu/~kriz/cifar-10-python.tar.gz to ./data/cifar-10-python.tar.gz

  0%|          | 0.00/170M [00:00<?, ?B/s]
  0%|          | 459k/170M [00:00<00:37, 4.59MB/s]
  4%|4         | 7.21M/170M [00:00<00:03, 41.6MB/s]
 10%|9         | 16.5M/170M [00:00<00:02, 65.0MB/s]
 16%|#5        | 27.1M/170M [00:00<00:01, 80.9MB/s]
 22%|##1       | 36.7M/170M [00:00<00:01, 86.6MB/s]
 27%|##7       | 46.5M/170M [00:00<00:01, 90.4MB/s]
 33%|###3      | 56.8M/170M [00:00<00:01, 94.2MB/s]
 39%|###8      | 66.2M/170M [00:00<00:01, 93.9MB/s]
 45%|####4     | 76.2M/170M [00:00<00:00, 95.7MB/s]
 51%|#####     | 86.2M/170M [00:01<00:00, 97.1MB/s]
 56%|#####6    | 95.9M/170M [00:01<00:00, 86.0MB/s]
 62%|######2   | 106M/170M [00:01<00:00, 90.6MB/s]
 68%|######7   | 116M/170M [00:01<00:00, 92.1MB/s]
 74%|#######4  | 126M/170M [00:01<00:00, 95.8MB/s]
 80%|#######9  | 136M/170M [00:01<00:00, 95.9MB/s]
 85%|########5 | 146M/170M [00:01<00:00, 96.0MB/s]
 92%|#########1| 156M/170M [00:01<00:00, 98.4MB/s]
 97%|#########7| 166M/170M [00:01<00:00, 97.1MB/s]
100%|##########| 170M/170M [00:01<00:00, 89.9MB/s]
Extracting ./data/cifar-10-python.tar.gz to ./data

Note

When you run the cell above, it may take a little time for the dataset to download.

This is an example of creating a dataset object in PyTorch. Downloadable datasets (like CIFAR-10 above) are subclasses of torch.utils.data.Dataset. Dataset classes in PyTorch include the downloadable datasets in TorchVision, Torchtext, and TorchAudio, as well as utility dataset classes such as torchvision.datasets.ImageFolder, which will read a folder of labeled images. You can also create your own subclasses of Dataset.

When we instantiate our dataset, we need to tell it a few things:

• The filesystem path to where we want the data to go.

• Whether or not we are using this set for training; most datasets will be split into training and test subsets.

• Whether we would like to download the dataset if we haven’t already.

• The transformations we want to apply to the data.

Once your dataset is ready, you can give it to the DataLoader:

trainloader = torch.utils.data.DataLoader(trainset, batch_size=4,
                                          shuffle=True, num_workers=2)

A Dataset subclass wraps access to the data, and is specialized to the type of data it’s serving. The DataLoader knows nothing about the data, but organizes the input tensors served by the Dataset into batches with the parameters you specify.

In the example above, we’ve asked a DataLoader to give us batches of 4 images from trainset, randomizing their order (shuffle=True), and we told it to spin up two workers to load data from disk.

It’s good practice to visualize the batches your DataLoader serves:

import matplotlib.pyplot as plt
import numpy as np

classes = ('plane', 'car', 'bird', 'cat',
           'deer', 'dog', 'frog', 'horse', 'ship', 'truck')

def imshow(img):
    img = img / 2 + 0.5     # unnormalize
    npimg = img.numpy()
    plt.imshow(np.transpose(npimg, (1, 2, 0)))


# get some random training images
dataiter = iter(trainloader)
images, labels = next(dataiter)

# show images
imshow(torchvision.utils.make_grid(images))
# print labels
print(' '.join('%5s' % classes[labels[j]] for j in range(4)))

Clipping input data to the valid range for imshow with RGB data ([0..1] for floats or [0..255] for integers). Got range [-0.49473685..1.5632443].
 ship   car horse  ship

Running the above cell should show you a strip of four images, and the correct label for each.

Training Your PyTorch Model

Follow along with the video beginning at 17:10.

Let’s put all the pieces together, and train a model:

#%matplotlib inline

import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim

import torchvision
import torchvision.transforms as transforms

import matplotlib
import matplotlib.pyplot as plt
import numpy as np

First, we’ll need training and test datasets. If you haven’t already, run the cell below to make sure the dataset is downloaded. (It may take a minute.)

transform = transforms.Compose(
    [transforms.ToTensor(),
     transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5))])

trainset = torchvision.datasets.CIFAR10(root='./data', train=True,
                                        download=True, transform=transform)
trainloader = torch.utils.data.DataLoader(trainset, batch_size=4,
                                          shuffle=True, num_workers=2)

testset = torchvision.datasets.CIFAR10(root='./data', train=False,
                                       download=True, transform=transform)
testloader = torch.utils.data.DataLoader(testset, batch_size=4,
                                         shuffle=False, num_workers=2)

classes = ('plane', 'car', 'bird', 'cat',
           'deer', 'dog', 'frog', 'horse', 'ship', 'truck')

Files already downloaded and verified
Files already downloaded and verified

We’ll run our check on the output from DataLoader:

import matplotlib.pyplot as plt
import numpy as np

# functions to show an image


def imshow(img):
    img = img / 2 + 0.5     # unnormalize
    npimg = img.numpy()
    plt.imshow(np.transpose(npimg, (1, 2, 0)))


# get some random training images
dataiter = iter(trainloader)
images, labels = next(dataiter)

# show images
imshow(torchvision.utils.make_grid(images))
# print labels
print(' '.join('%5s' % classes[labels[j]] for j in range(4)))

cat   cat  deer  frog

This is the model we’ll train. If it looks familiar, that’s because it’s a variant of LeNet - discussed earlier in this video - adapted for 3-color images.

class Net(nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        self.conv1 = nn.Conv2d(3, 6, 5)
        self.pool = nn.MaxPool2d(2, 2)
        self.conv2 = nn.Conv2d(6, 16, 5)
        self.fc1 = nn.Linear(16 * 5 * 5, 120)
        self.fc2 = nn.Linear(120, 84)
        self.fc3 = nn.Linear(84, 10)

    def forward(self, x):
        x = self.pool(F.relu(self.conv1(x)))
        x = self.pool(F.relu(self.conv2(x)))
        x = x.view(-1, 16 * 5 * 5)
        x = F.relu(self.fc1(x))
        x = F.relu(self.fc2(x))
        x = self.fc3(x)
        return x


net = Net()

The last ingredients we need are a loss function and an optimizer:

criterion = nn.CrossEntropyLoss()
optimizer = optim.SGD(net.parameters(), lr=0.001, momentum=0.9)

The loss function, as discussed earlier in this video, is a measure of how far from our ideal output the model’s prediction was. Cross-entropy loss is a typical loss function for classification models like ours.

The optimizer is what drives the learning. Here we have created an optimizer that implements stochastic gradient descent, one of the more straightforward optimization algorithms. Besides parameters of the algorithm, like the learning rate (lr) and momentum, we also pass in net.parameters(), which is a collection of all the learning weights in the model - which is what the optimizer adjusts.

Finally, all of this is assembled into the training loop. Go ahead and run this cell, as it will likely take a few minutes to execute:

for epoch in range(2):  # loop over the dataset multiple times

    running_loss = 0.0
    for i, data in enumerate(trainloader, 0):
        # get the inputs
        inputs, labels = data

        # zero the parameter gradients
        optimizer.zero_grad()

        # forward + backward + optimize
        outputs = net(inputs)
        loss = criterion(outputs, labels)
        loss.backward()
        optimizer.step()

        # print statistics
        running_loss += loss.item()
        if i % 2000 == 1999:    # print every 2000 mini-batches
            print('[%d, %5d] loss: %.3f' %
                  (epoch + 1, i + 1, running_loss / 2000))
            running_loss = 0.0

print('Finished Training')

[1,  2000] loss: 2.195
[1,  4000] loss: 1.876
[1,  6000] loss: 1.655
[1,  8000] loss: 1.576
[1, 10000] loss: 1.519
[1, 12000] loss: 1.466
[2,  2000] loss: 1.421
[2,  4000] loss: 1.376
[2,  6000] loss: 1.336
[2,  8000] loss: 1.335
[2, 10000] loss: 1.326
[2, 12000] loss: 1.270
Finished Training

Here, we are doing only 2 training epochs (line 1) - that is, two passes over the training dataset. Each pass has an inner loop that iterates over the training data (line 4), serving batches of transformed input images and their correct labels.

Zeroing the gradients (line 9) is an important step. Gradients are accumulated over a batch; if we do not reset them for every batch, they will keep accumulating, which will provide incorrect gradient values, making learning impossible.

In line 12, we ask the model for its predictions on this batch. In the following line (13), we compute the loss - the difference between outputs (the model prediction) and labels (the correct output).

In line 14, we do the backward() pass, and calculate the gradients that will direct the learning.

In line 15, the optimizer performs one learning step - it uses the gradients from the backward() call to nudge the learning weights in the direction it thinks will reduce the loss.

The remainder of the loop does some light reporting on the epoch number, how many training instances have been completed, and what the collected loss is over the training loop.

When you run the cell above, you should see something like this:

[1,  2000] loss: 2.235
[1,  4000] loss: 1.940
[1,  6000] loss: 1.713
[1,  8000] loss: 1.573
[1, 10000] loss: 1.507
[1, 12000] loss: 1.442
[2,  2000] loss: 1.378
[2,  4000] loss: 1.364
[2,  6000] loss: 1.349
[2,  8000] loss: 1.319
[2, 10000] loss: 1.284
[2, 12000] loss: 1.267
Finished Training

Note that the loss is monotonically descending, indicating that our model is continuing to improve its performance on the training dataset.

As a final step, we should check that the model is actually doing general learning, and not simply “memorizing” the dataset. This is called overfitting, and usually indicates that the dataset is too small (not enough examples for general learning), or that the model has more learning parameters than it needs to correctly model the dataset.

This is the reason datasets are split into training and test subsets - to test the generality of the model, we ask it to make predictions on data it hasn’t trained on:

correct = 0
total = 0
with torch.no_grad():
    for data in testloader:
        images, labels = data
        outputs = net(images)
        _, predicted = torch.max(outputs.data, 1)
        total += labels.size(0)
        correct += (predicted == labels).sum().item()

print('Accuracy of the network on the 10000 test images: %d %%' % (
    100 * correct / total))

Accuracy of the network on the 10000 test images: 54 %

If you followed along, you should see that the model is roughly 50% accurate at this point. That’s not exactly state-of-the-art, but it’s far better than the 10% accuracy we’d expect from a random output. This demonstrates that some general learning did happen in the model.