Hooks for autograd saved tensors

Created On: Nov 03, 2021 | Last Updated: Aug 27, 2024 | Last Verified: Not Verified

PyTorch typically computes gradients using backpropagation. However, certain operations require intermediary results to be saved in order to perform backpropagation. This tutorial walks through how these tensors are saved/retrieved and how you can define hooks to control the packing/unpacking process.

This tutorial assumes you are familiar with how backpropagation works in theory. If not, read this first.

Saved tensors

Training a model usually consumes more memory than running it for inference. Broadly speaking, one can say that it is because “PyTorch needs to save the computation graph, which is needed to call backward”, hence the additional memory usage. One goal of this tutorial is to finetune this understanding.

In fact, the graph in itself sometimes does not consume much more memory as it never copies any tensors. However, the graph can keep references to tensors that would otherwise have gone out of scope: those are referred to as saved tensors.

Why does training a model (typically) requires more memory than evaluating it?

We start with a simple example: \(y = a \cdot b\) , for which we know the gradients of \(y\) with respect to \(a\) and \(b\):

\[\frac{\partial y}{\partial a} = b \]

\[\frac{\partial y}{\partial b} = a \]

import torch

a = torch.randn(5, requires_grad=True)
b = torch.ones(5, requires_grad=True)
y = a * b

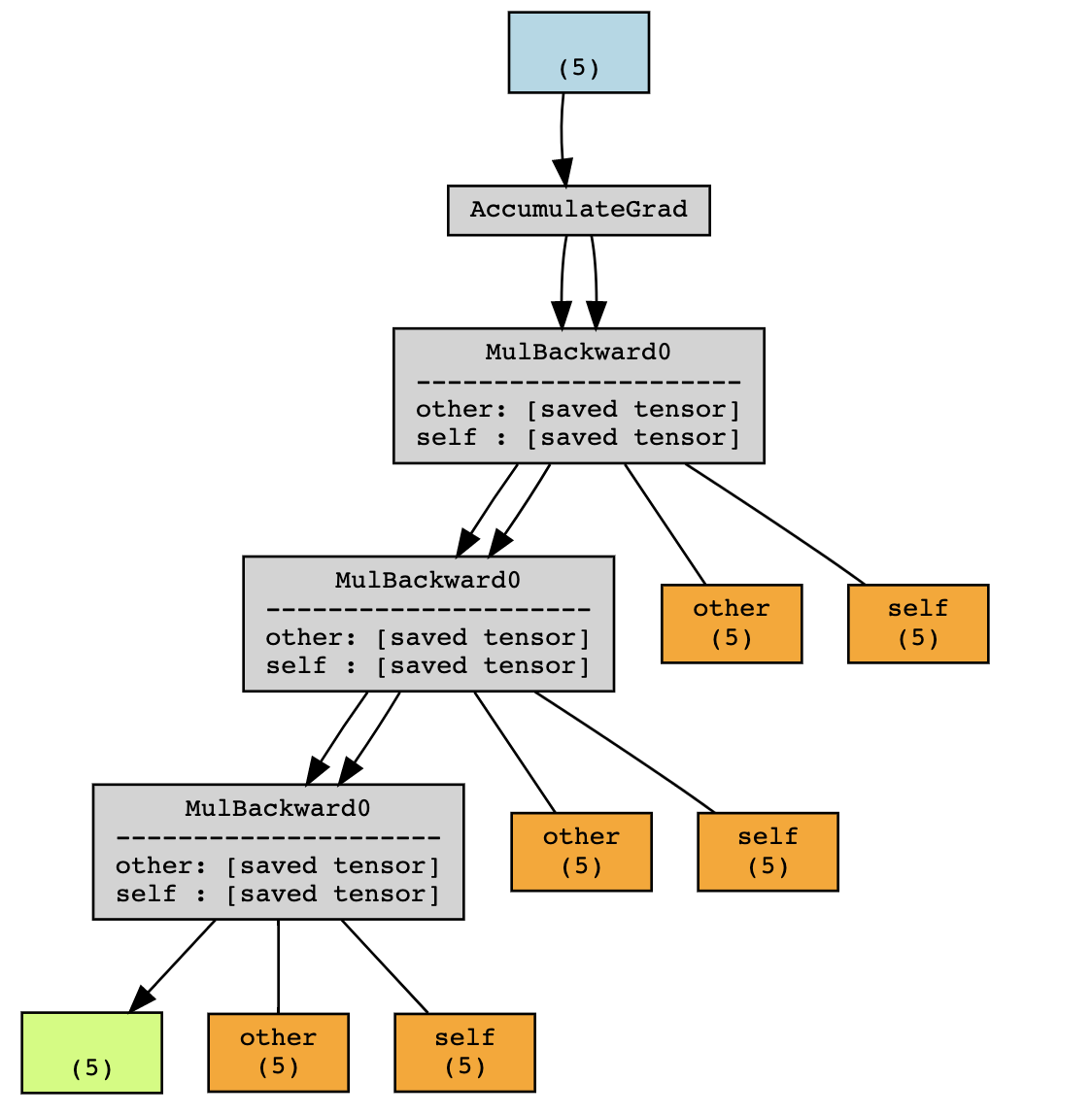
Using a torchviz, we can visualize the computation graph

In this example, PyTorch saves intermediary values \(a\) and \(b\) in order to compute the gradient during the backward.

Those intermediary values (in orange above) can be accessed (for debugging purposes) by looking for attributes of the grad_fn of y which start with the prefix _saved:

print(y.grad_fn._saved_self)
print(y.grad_fn._saved_other)

tensor([ 0.3367,  0.1288,  0.2345,  0.2303, -1.1229], requires_grad=True)
tensor([1., 1., 1., 1., 1.], requires_grad=True)

As the computation graph grows in depth, it will store more saved tensors. Meanwhile, those tensors would have gone out of scope if not for the graph.

def f(x):
    return x * x

x = torch.randn(5, requires_grad=True)
y = f(f(f(x)))

In the example above, executing without grad would only have kept x and y in the scope, But the graph additionally stores f(x) and f(f(x)). Hence, running a forward pass during training will be more costly in memory usage than during evaluation (more precisely, when autograd is not required).

The concept of packing / unpacking

Going back to the first example: y.grad_fn._saved_self and y.grad_fn._saved_other point to the original tensor object, respectively a and b.

a = torch.randn(5, requires_grad=True)
b = torch.ones(5, requires_grad=True)
y = a * b

print(y.grad_fn._saved_self is a)   # True
print(y.grad_fn._saved_other is b)  # True

True
True

However, that may not always be the case.

a = torch.randn(5, requires_grad=True)
y = torch.exp(a)
print(y.grad_fn._saved_result.equal(y))  # True
print(y.grad_fn._saved_result is y)      # False

True
False

Under the hood, PyTorch has packed and unpacked the tensor y to prevent reference cycles.

As a rule of thumb, you should not rely on the fact that accessing the tensor saved for backward will yield the same tensor object as the original tensor. They will however share the same storage.

Saved tensors hooks

PyTorch provides an API to control how saved tensors should be packed / unpacked.

def pack_hook(x):
    print("Packing", x)
    return x

def unpack_hook(x):
    print("Unpacking", x)
    return x
a = torch.ones(5, requires_grad=True)
b = torch.ones(5, requires_grad=True) * 2

with torch.autograd.graph.saved_tensors_hooks(pack_hook, unpack_hook):
    y = a * b

y.sum().backward()

Packing tensor([2., 2., 2., 2., 2.], grad_fn=<MulBackward0>)
Packing tensor([1., 1., 1., 1., 1.], requires_grad=True)
Unpacking tensor([2., 2., 2., 2., 2.], grad_fn=<MulBackward0>)
Unpacking tensor([1., 1., 1., 1., 1.], requires_grad=True)

The pack_hook function will be called every time an operation saves a tensor for backward. The output of pack_hook is then stored in the computation graph instead of the original tensor. The unpack_hook uses that return value to compute a new tensor, which is the one actually used during the backward pass. In general, you want unpack_hook(pack_hook(t)) to be equal to t.

x = torch.randn(5, requires_grad=True)
with torch.autograd.graph.saved_tensors_hooks(lambda x: x * 4, lambda x: x / 4):
    y = torch.pow(x, 2)
y.sum().backward()
assert(x.grad.equal(2 * x))

One thing to note is that the output of pack_hook can be any Python object, as long as unpack_hook can derive a tensor with the correct value from it.

Some unconventional examples

First, some silly examples to illustrate what is possible but you probably don’t ever want to do it.

Returning an int

Returning the index of a Python list Relatively harmless but with debatable usefulness

storage = []

def pack(x):
    storage.append(x)
    return len(storage) - 1

def unpack(x):
    return storage[x]

x = torch.randn(5, requires_grad=True)
with torch.autograd.graph.saved_tensors_hooks(pack, unpack):
    y = x * x
y.sum().backward()

assert(x.grad.equal(2 * x))

Returning a tuple

Returning some tensor and a function how to unpack it Quite unlikely to be useful in its current form

def pack(x):
    delta = torch.randn(*x.size())
    return x - delta, lambda x: x + delta

def unpack(packed):
    x, f = packed
    return f(x)


x = torch.randn(5, requires_grad=True)
with torch.autograd.graph.saved_tensors_hooks(pack, unpack):
    y = x * x
y.sum().backward()

assert(torch.allclose(x.grad, 2 * x))

Returning a str

Returning the __repr__ of the tensor Probably never do this

x = torch.randn(5, requires_grad=True)
with torch.autograd.graph.saved_tensors_hooks(lambda x: repr(x), lambda x: eval("torch." + x)):
    y = x * x
y.sum().backward()
assert(torch.all(x.grad - 2 * x <= 1e-4))

Although those examples will not be useful in practice, they illustrate that the output of pack_hook can really be any Python object as long as it contains enough information to retrieve the content of the original tensor. In the next sections, we focus on more useful applications.

Saving tensors to CPU

Very often, the tensors involved in the computation graph live on GPU. Keeping a reference to those tensors in the graph is what causes most models to run out of GPU memory during training while they would have done fine during evaluation.

Hooks provide a very simple way to implement that.

def pack_hook(x):
    return (x.device, x.cpu())

def unpack_hook(packed):
    device, tensor = packed
    return tensor.to(device)

x = torch.randn(5, requires_grad=True)
with torch.autograd.graph.saved_tensors_hooks(pack, unpack):
    y = x * x
y.sum().backward()

torch.allclose(x.grad, (2 * x))

True

In fact, PyTorch provides an API to conveniently use those hooks (as well as the ability to use pinned memory).

import torch.nn as nn

class Model(nn.Module):
    def __init__(self):
        super().__init__()
        self.w = nn.Parameter(torch.randn(5))

    def forward(self, x):
        with torch.autograd.graph.save_on_cpu(pin_memory=True):
            # some computation
            return self.w * x

x = torch.randn(5)
model = Model()
loss = model(x).sum()
loss.backward()

In practice, on a A100 GPU, for a ResNet-152 with batch size 256, this corresponds to a GPU memory usage reduction from 48GB to 5GB, at the cost of a 6x slowdown.

Of course, you can modulate the tradeoff by only saving to CPU certain parts of the network.

For instance, you could define a special nn.Module that wraps any module and saves its tensors to CPU.

class SaveToCpu(nn.Module):
    def __init__(self, module):
        super().__init__()
        self.module = module

    def forward(self, *args, **kwargs):
        with torch.autograd.graph.save_on_cpu(pin_memory=True):
            return self.module(*args, **kwargs)

model = nn.Sequential(
    nn.Linear(10, 100),
    SaveToCpu(nn.Linear(100, 100)),
    nn.Linear(100, 10),
)

x = torch.randn(10)
loss = model(x).sum()
loss.backward()

Saving tensors to disk

Similarly, you may want to save those tensors to disk. Again, this is achievable with those hooks.

A naive version would look like this.

# Naive version - HINT: Don't do this

import uuid
tmp_dir = "temp"

def pack_hook(tensor):
    name = os.path.join(tmp_dir, str(uuid.uuid4()))
    torch.save(tensor, name)
    return name

def unpack_hook(name):
    return torch.load(name, weights_only=True)

The reason the above code is bad is that we are leaking files on the disk and they are never cleared. Fixing this is not as trivial as it seems.

# Incorrect version - HINT: Don't do this

import uuid
import os
import tempfile
tmp_dir_obj = tempfile.TemporaryDirectory()
tmp_dir = tmp_dir_obj.name

def pack_hook(tensor):
    name = os.path.join(tmp_dir, str(uuid.uuid4()))
    torch.save(tensor, name)
    return name

def unpack_hook(name):
    tensor = torch.load(name, weights_only=True)
    os.remove(name)
    return tensor

The reason the above code doesn’t work is that unpack_hook can be called multiple times. If we delete the file during unpacking the first time, it will not be available when the saved tensor is accessed a second time, which will raise an error.

x = torch.ones(5, requires_grad=True)
with torch.autograd.graph.saved_tensors_hooks(pack_hook, unpack_hook):
    y = x.pow(2)
print(y.grad_fn._saved_self)
try:
    print(y.grad_fn._saved_self)
    print("Double access succeeded!")
except:
    print("Double access failed!")

tensor([1., 1., 1., 1., 1.], requires_grad=True)
Double access failed!

To fix this, we can write a version of those hooks that takes advantage of the fact that PyTorch automatically releases (deletes) the saved data when it is no longer needed.

class SelfDeletingTempFile():
    def __init__(self):
        self.name = os.path.join(tmp_dir, str(uuid.uuid4()))

    def __del__(self):
        os.remove(self.name)

def pack_hook(tensor):
    temp_file = SelfDeletingTempFile()
    torch.save(tensor, temp_file.name)
    return temp_file

def unpack_hook(temp_file):
    return torch.load(temp_file.name, weights_only=True)

When we call backward, the output of pack_hook will be deleted, which causes the file to be removed, so we’re no longer leaking the files.

This can then be used in your model, in the following way:

# Only save on disk tensors that have size >= 1000
SAVE_ON_DISK_THRESHOLD = 1000

def pack_hook(x):
    if x.numel() < SAVE_ON_DISK_THRESHOLD:
        return x
    temp_file = SelfDeletingTempFile()
    torch.save(tensor, temp_file.name)
    return temp_file

def unpack_hook(tensor_or_sctf):
    if isinstance(tensor_or_sctf, torch.Tensor):
        return tensor_or_sctf
    return torch.load(tensor_or_sctf.name)

class SaveToDisk(nn.Module):
    def __init__(self, module):
        super().__init__()
        self.module = module

    def forward(self, *args, **kwargs):
        with torch.autograd.graph.saved_tensors_hooks(pack_hook, unpack_hook):
            return self.module(*args, **kwargs)

net = nn.DataParallel(SaveToDisk(Model()))

In this last example, we also demonstrate how to filter which tensors should be saved (here, those whose number of elements is greater than 1000) and how to combine this feature with nn.DataParallel.

If you’ve made it this far, congratulations! You now know how to use saved tensor hooks and how they can be useful in a few scenarios to tradeoff memory for compute.