Note
Click here to download the full example code
Filter design tutorial
Author: Moto Hira
This tutorial shows how to create basic digital filters (impulse responses) and their properties.
We look into low-pass, high-pass and band-pass filters based on windowed-sinc kernels, and frequency sampling method.
Warning
This tutorial requires prototype DSP features, which are available in nightly builds.
Please refer to https://pytorch.org/get-started/locally for instructions for installing a nightly build.
import torch
import torchaudio
print(torch.__version__)
print(torchaudio.__version__)
import matplotlib.pyplot as plt
2.6.0.dev20241104
2.5.0.dev20241105
from torchaudio.prototype.functional import frequency_impulse_response, sinc_impulse_response
Windowed-Sinc Filter
Sinc filter is an idealized filter which removes frequencies above the cutoff frequency without affecting the lower frequencies.
Sinc filter has infinite filter width in analytical solution. In numerical computation, sinc filter cannot be expressed exactly, so an approximation is required.
Windowed-sinc finite impulse response is an approximation of sinc filter. It is obtained by first evaluating sinc function for given cutoff frequencies, then truncating the filter skirt, and applying a window, such as Hamming window, to reduce the artifacts introduced from the truncation.
sinc_impulse_response()
generates windowed-sinc impulse response for given cutoff
frequencies.
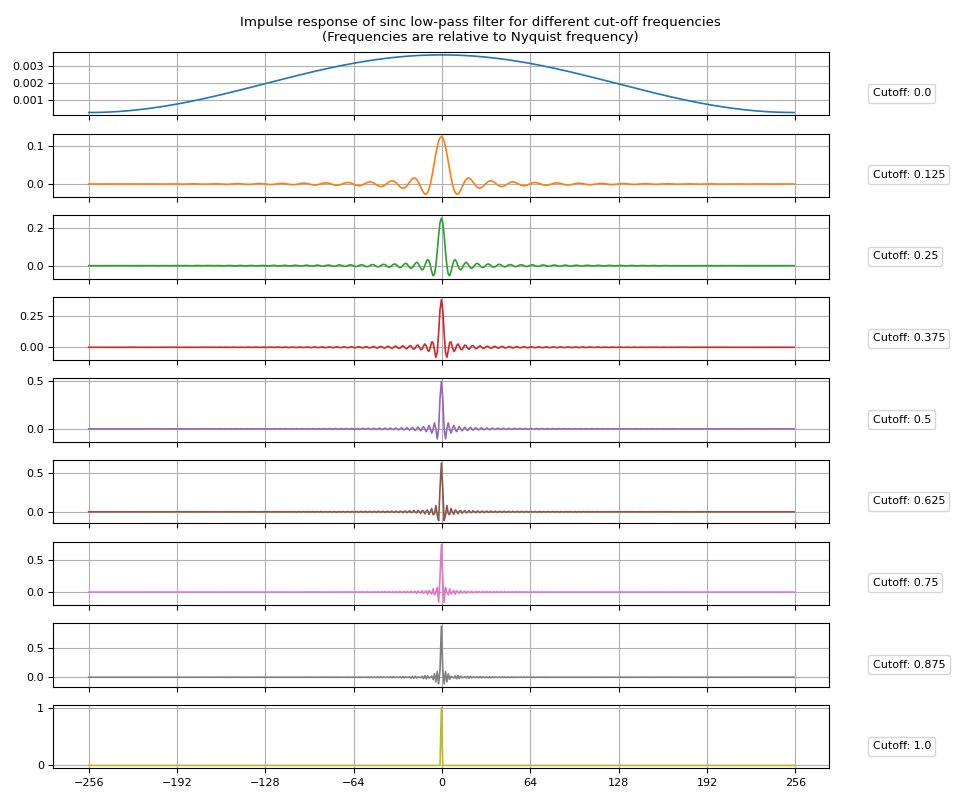
Low-pass filter
Impulse Response
Creating sinc IR is as easy as passing cutoff frequency values to
sinc_impulse_response().
cutoff = torch.linspace(0.0, 1.0, 9)
irs = sinc_impulse_response(cutoff, window_size=513)
print("Cutoff shape:", cutoff.shape)
print("Impulse response shape:", irs.shape)
Cutoff shape: torch.Size([9])
Impulse response shape: torch.Size([9, 513])
Let’s visualize the resulting impulse responses.
def plot_sinc_ir(irs, cutoff):
num_filts, window_size = irs.shape
half = window_size // 2
fig, axes = plt.subplots(num_filts, 1, sharex=True, figsize=(9.6, 8))
t = torch.linspace(-half, half - 1, window_size)
for ax, ir, coff, color in zip(axes, irs, cutoff, plt.cm.tab10.colors):
ax.plot(t, ir, linewidth=1.2, color=color, zorder=4, label=f"Cutoff: {coff}")
ax.legend(loc=(1.05, 0.2), handletextpad=0, handlelength=0)
ax.grid(True)
fig.suptitle(
"Impulse response of sinc low-pass filter for different cut-off frequencies\n"
"(Frequencies are relative to Nyquist frequency)"
)
axes[-1].set_xticks([i * half // 4 for i in range(-4, 5)])
fig.tight_layout()
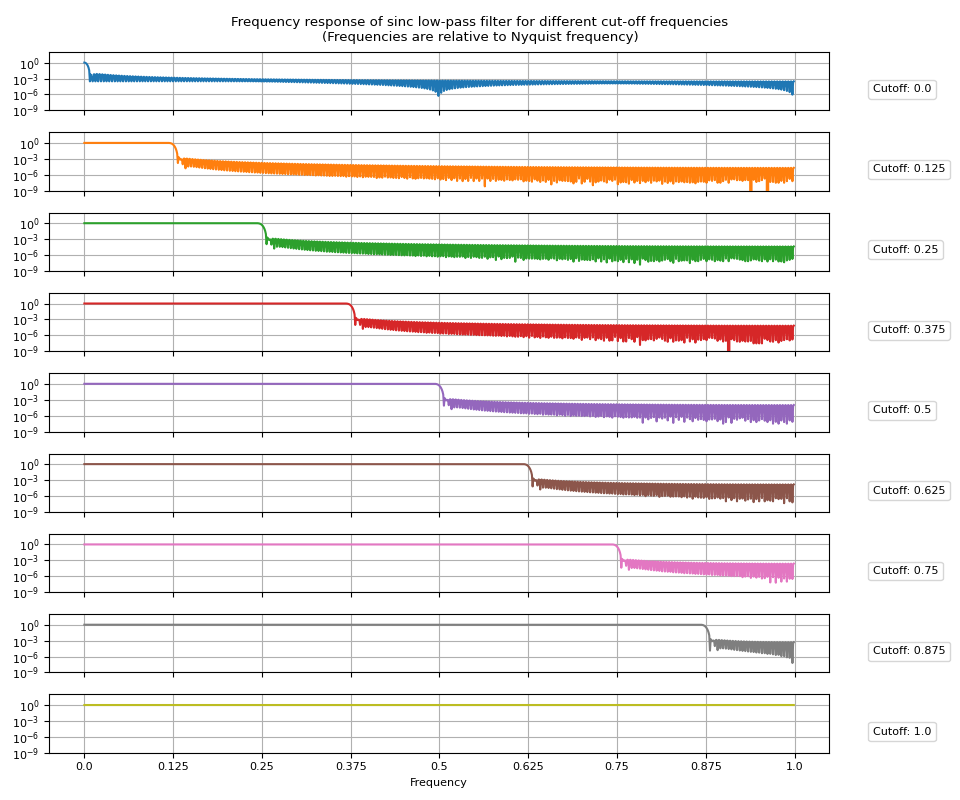
Frequency Response
Next, let’s look at the frequency responses. Simpy applying Fourier transform to the impulse responses will give the frequency responses.
frs = torch.fft.rfft(irs, n=2048, dim=1).abs()
Let’s visualize the resulting frequency responses.
def plot_sinc_fr(frs, cutoff, band=False):
num_filts, num_fft = frs.shape
num_ticks = num_filts + 1 if band else num_filts
fig, axes = plt.subplots(num_filts, 1, sharex=True, sharey=True, figsize=(9.6, 8))
for ax, fr, coff, color in zip(axes, frs, cutoff, plt.cm.tab10.colors):
ax.grid(True)
ax.semilogy(fr, color=color, zorder=4, label=f"Cutoff: {coff}")
ax.legend(loc=(1.05, 0.2), handletextpad=0, handlelength=0).set_zorder(3)
axes[-1].set(
ylim=[None, 100],
yticks=[1e-9, 1e-6, 1e-3, 1],
xticks=torch.linspace(0, num_fft, num_ticks),
xticklabels=[f"{i/(num_ticks - 1)}" for i in range(num_ticks)],
xlabel="Frequency",
)
fig.suptitle(
"Frequency response of sinc low-pass filter for different cut-off frequencies\n"
"(Frequencies are relative to Nyquist frequency)"
)
fig.tight_layout()
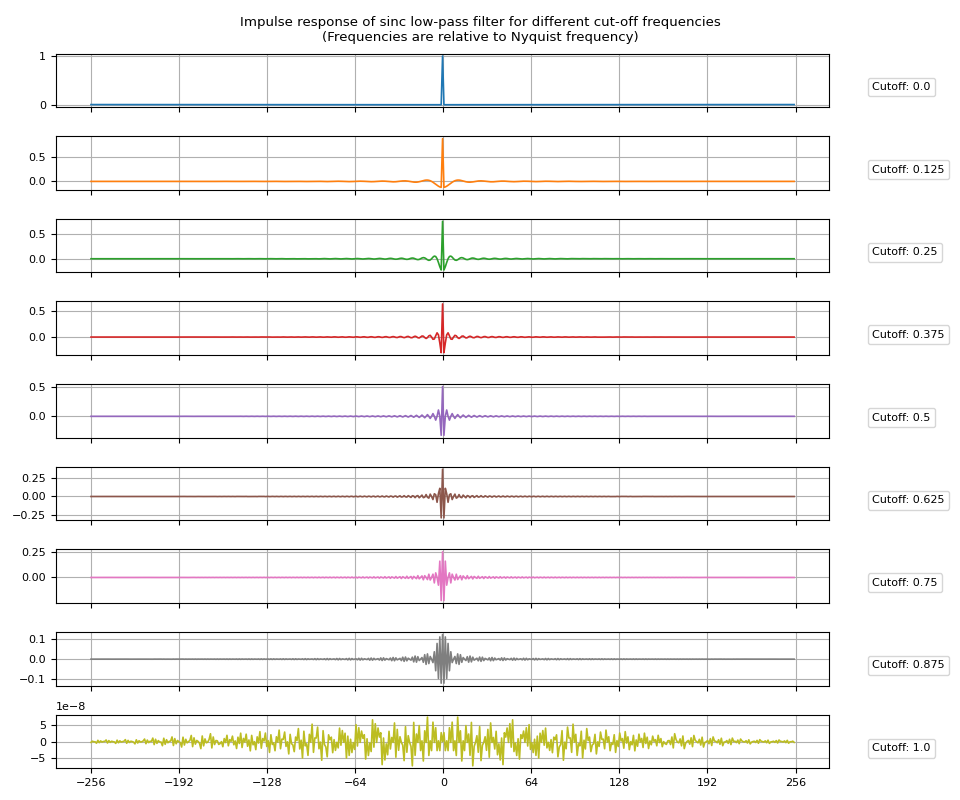
High-pass filter
High-pass filter can be obtained by subtracting low-pass impulse response from the Dirac delta function.
Passing high_pass=True to
sinc_impulse_response()
will change the returned filter kernel to high pass filter.
irs = sinc_impulse_response(cutoff, window_size=513, high_pass=True)
frs = torch.fft.rfft(irs, n=2048, dim=1).abs()
Impulse Response
Frequency Response
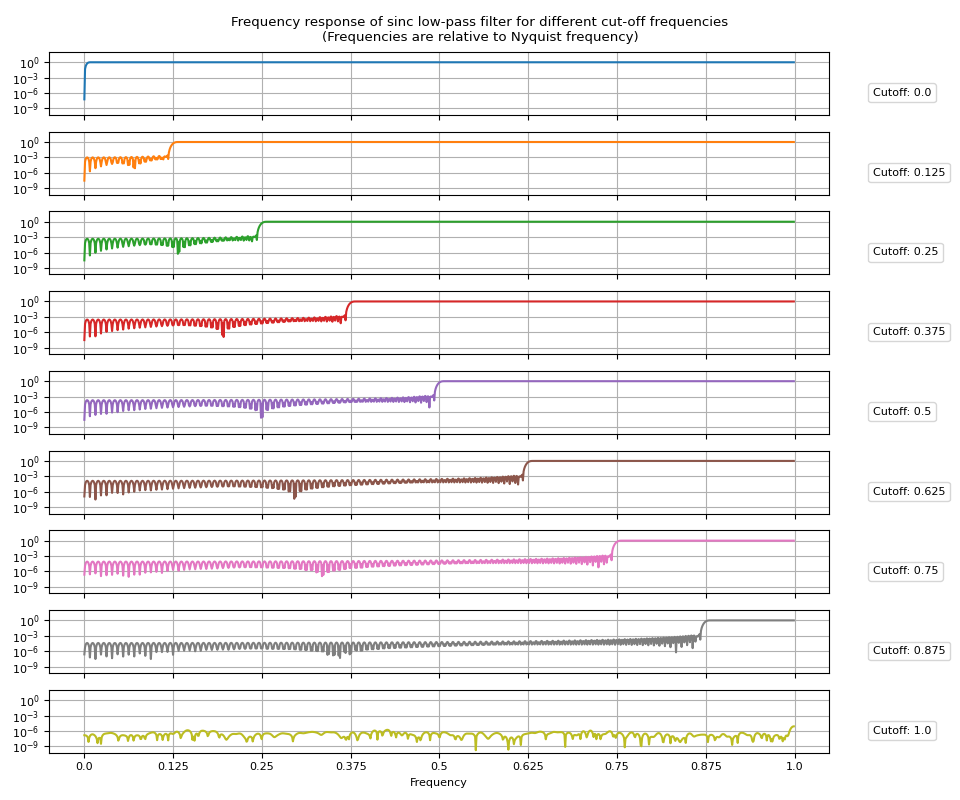
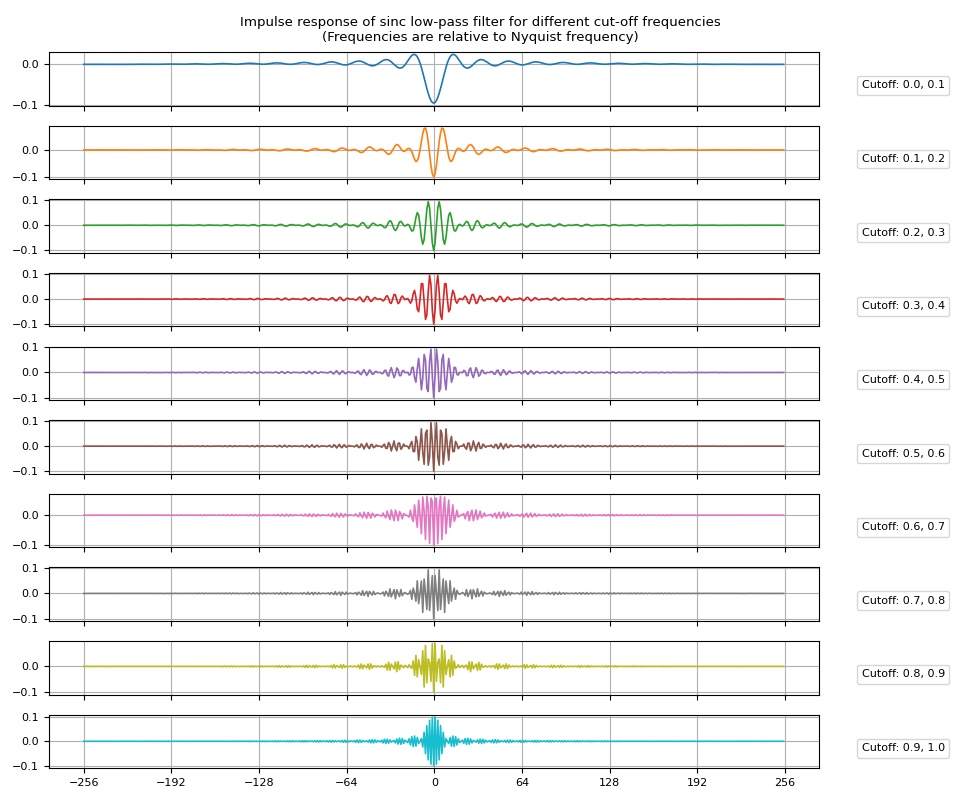
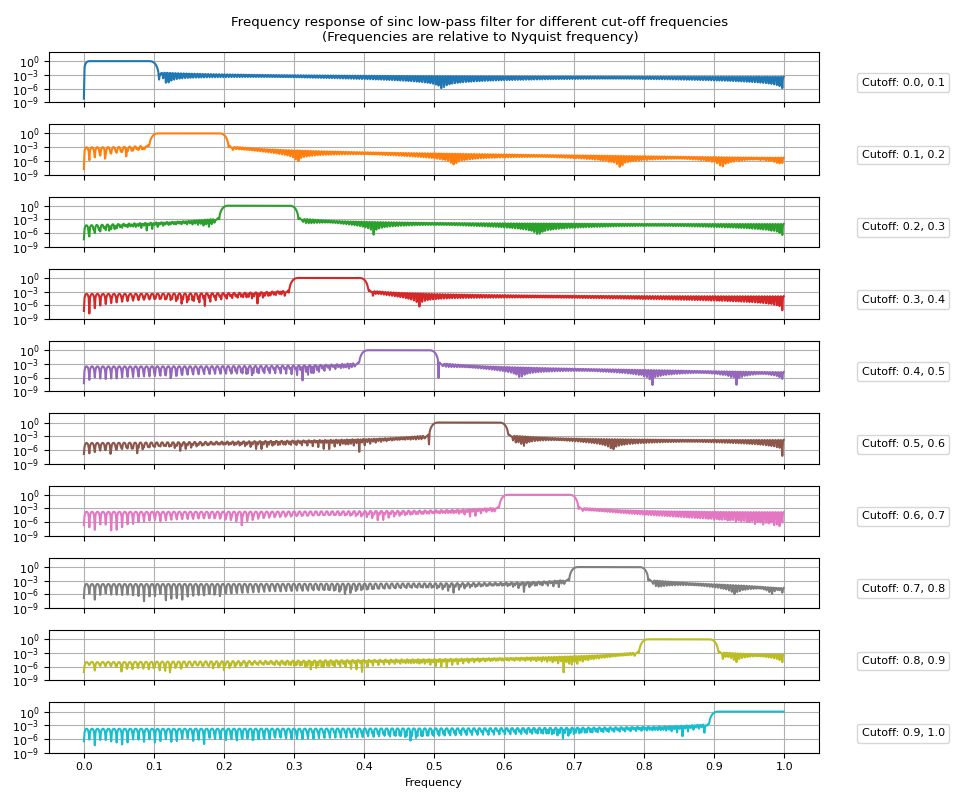
Band-pass filter
Band-pass filter can be obtained by subtracting low-pass filter for upper band from that of lower band.
Impulse Response
Frequency Response
Frequency Sampling
The next method we look into starts from a desired frequency response and obtain impulse response by applying inverse Fourier transform.
frequency_impulse_response()
takes (unnormalized) magnitude distribution of frequencies and
construct impulse response from it.
Note however that the resulting impulse response does not produce the desired frequency response.
In the following, we create multiple filters and compare the input frequency response and the actual frequency response.
Brick-wall filter
Let’s start from brick-wall filter
magnitudes = torch.concat([torch.ones((128,)), torch.zeros((128,))])
ir = frequency_impulse_response(magnitudes)
print("Magnitudes:", magnitudes.shape)
print("Impulse Response:", ir.shape)
Magnitudes: torch.Size([256])
Impulse Response: torch.Size([510])
def plot_ir(magnitudes, ir, num_fft=2048):
fr = torch.fft.rfft(ir, n=num_fft, dim=0).abs()
ir_size = ir.size(-1)
half = ir_size // 2
fig, axes = plt.subplots(3, 1)
t = torch.linspace(-half, half - 1, ir_size)
axes[0].plot(t, ir)
axes[0].grid(True)
axes[0].set(title="Impulse Response")
axes[0].set_xticks([i * half // 4 for i in range(-4, 5)])
t = torch.linspace(0, 1, fr.numel())
axes[1].plot(t, fr, label="Actual")
axes[2].semilogy(t, fr, label="Actual")
t = torch.linspace(0, 1, magnitudes.numel())
for i in range(1, 3):
axes[i].plot(t, magnitudes, label="Desired (input)", linewidth=1.1, linestyle="--")
axes[i].grid(True)
axes[1].set(title="Frequency Response")
axes[2].set(title="Frequency Response (log-scale)", xlabel="Frequency")
axes[2].legend(loc="center right")
fig.tight_layout()
plot_ir(magnitudes, ir)
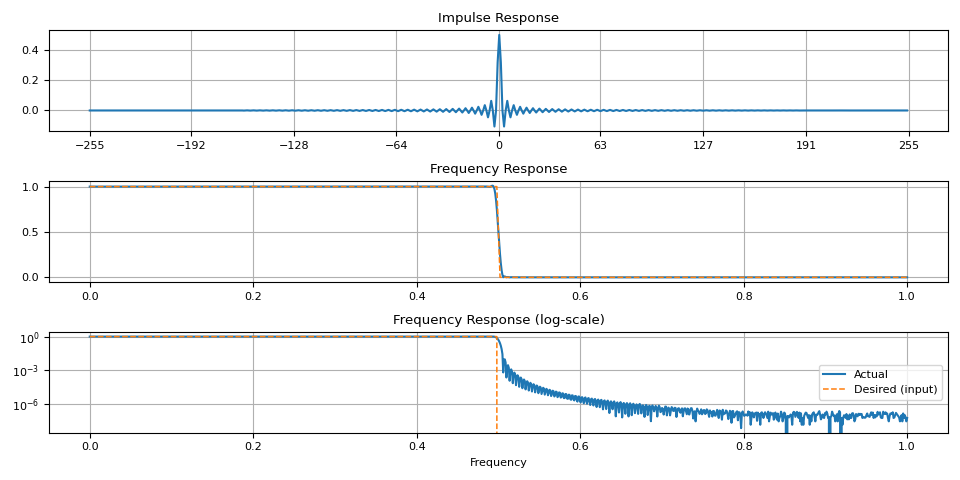
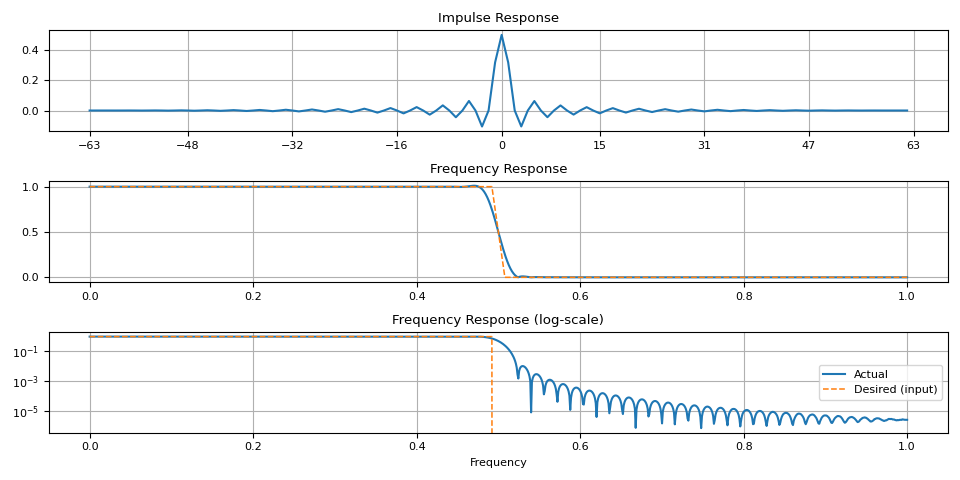
Notice that there are artifacts around the transition band. This is more noticeable when the window size is small.
magnitudes = torch.concat([torch.ones((32,)), torch.zeros((32,))])
ir = frequency_impulse_response(magnitudes)
plot_ir(magnitudes, ir)
Arbitrary shapes
magnitudes = torch.linspace(0, 1, 64) ** 4.0
ir = frequency_impulse_response(magnitudes)
plot_ir(magnitudes, ir)
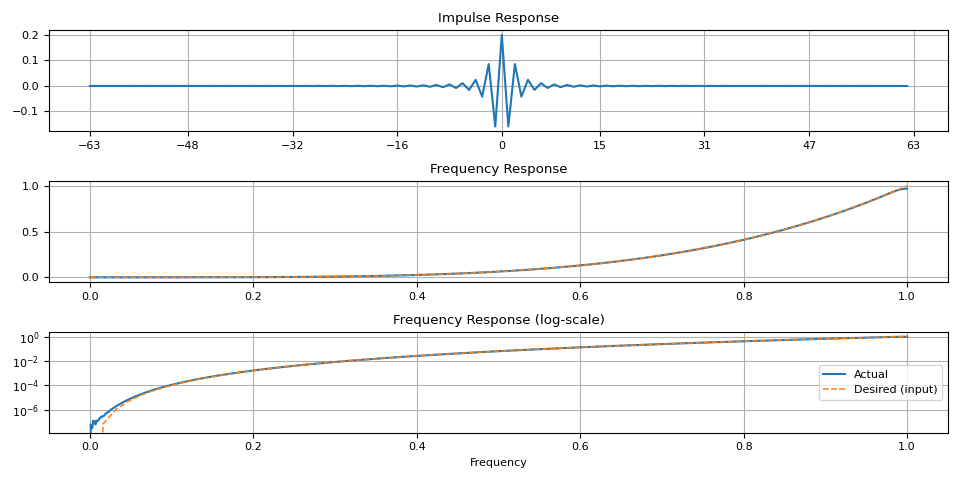
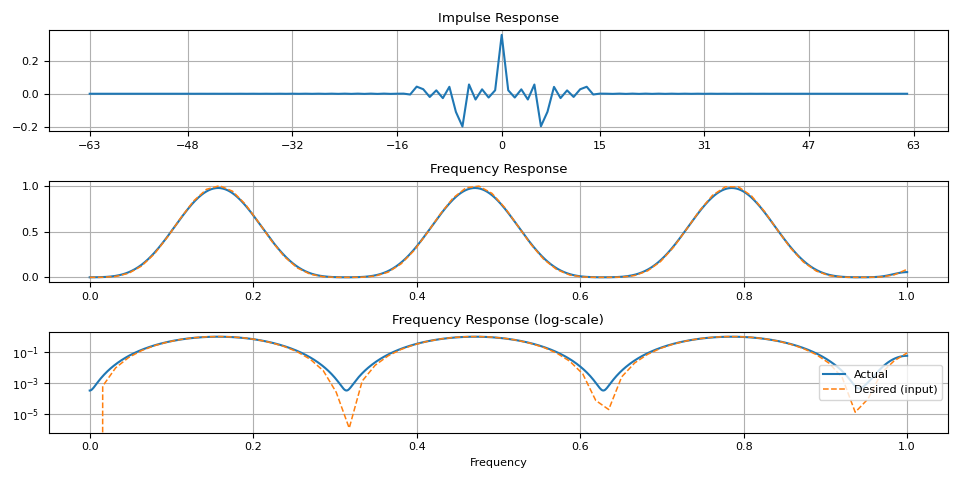
magnitudes = torch.sin(torch.linspace(0, 10, 64)) ** 4.0
ir = frequency_impulse_response(magnitudes)
plot_ir(magnitudes, ir)
References
https://www.analog.com/media/en/technical-documentation/dsp-book/dsp_book_Ch16.pdf
https://courses.engr.illinois.edu/ece401/fa2020/slides/lec10.pdf
https://ccrma.stanford.edu/~jos/sasp/Windowing_Desired_Impulse_Response.html
Total running time of the script: ( 0 minutes 5.220 seconds)



