Additive Synthesis

Author: Moto Hira

This tutorial is the continuation of Oscillator and ADSR Envelope.

This tutorial shows how to perform additive synthesis and subtractive synthesis using TorchAudio’s DSP functions.

Additive synthesis creates timbre by combining multiple waveform. Subtractive synthesis creates timbre by applying filters.

Warning

This tutorial requires prototype DSP features, which are available in nightly builds.

Please refer to https://pytorch.org/get-started/locally for instructions for installing a nightly build.

import torch
import torchaudio

print(torch.__version__)
print(torchaudio.__version__)

2.4.0.dev20240419
2.2.0.dev20240420

Overview

try:
    from torchaudio.prototype.functional import adsr_envelope, extend_pitch, oscillator_bank
except ModuleNotFoundError:
    print(
        "Failed to import prototype DSP features. "
        "Please install torchaudio nightly builds. "
        "Please refer to https://pytorch.org/get-started/locally "
        "for instructions to install a nightly build."
    )
    raise

import matplotlib.pyplot as plt
from IPython.display import Audio

Creating multiple frequency pitches

The core of additive synthesis is oscillator. We create a timbre by summing up the multiple waveforms generated by oscillator.

In the oscillator tutorial, we used oscillator_bank() and adsr_envelope() to generate various waveforms.

In this tutorial, we use extend_pitch() to create a timbre from base frequency.

First, we define some constants and helper function that we use throughout the tutorial.

PI = torch.pi
PI2 = 2 * torch.pi

F0 = 344.0  # fundamental frequency
DURATION = 1.1  # [seconds]
SAMPLE_RATE = 16_000  # [Hz]

NUM_FRAMES = int(DURATION * SAMPLE_RATE)

def plot(freq, amp, waveform, sample_rate, zoom=None, vol=0.1):
    t = (torch.arange(waveform.size(0)) / sample_rate).numpy()

    fig, axes = plt.subplots(4, 1, sharex=True)
    axes[0].plot(t, freq.numpy())
    axes[0].set(title=f"Oscillator bank (bank size: {amp.size(-1)})", ylabel="Frequency [Hz]", ylim=[-0.03, None])
    axes[1].plot(t, amp.numpy())
    axes[1].set(ylabel="Amplitude", ylim=[-0.03 if torch.all(amp >= 0.0) else None, None])
    axes[2].plot(t, waveform)
    axes[2].set(ylabel="Waveform")
    axes[3].specgram(waveform, Fs=sample_rate)
    axes[3].set(ylabel="Spectrogram", xlabel="Time [s]", xlim=[-0.01, t[-1] + 0.01])

    for i in range(4):
        axes[i].grid(True)
    pos = axes[2].get_position()
    fig.tight_layout()

    if zoom is not None:
        ax = fig.add_axes([pos.x0 + 0.02, pos.y0 + 0.03, pos.width / 2.5, pos.height / 2.0])
        ax.plot(t, waveform)
        ax.set(xlim=zoom, xticks=[], yticks=[])

    waveform /= waveform.abs().max()
    return Audio(vol * waveform, rate=sample_rate, normalize=False)

Harmonic Overtones

Harmonic overtones are frequency components that are an integer multiple of the fundamental frequency.

We look at how to generate the common waveforms that are used in synthesizers. That is,

• Sawtooth wave

• Square wave

• Triangle wave

Sawtooth wave

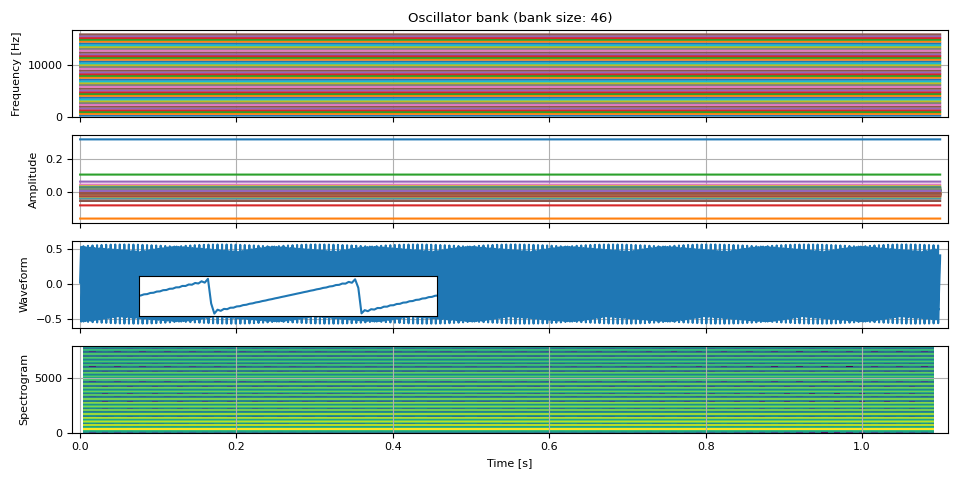
Sawtooth wave can be expressed as the following. It contains all the integer harmonics, so it is commonly used in subtractive synthesis as well.

\[\begin{align*} y_t &= \sum_{k=1}^{K} A_k \sin ( 2 \pi f_k t ) \\ \text{where} \\ f_k &= k f_0 \\ A_k &= -\frac{ (-1) ^k }{k \pi} \end{align*}\]

The following function takes fundamental frequencies and amplitudes, and adds extend pitch in accordance with the formula above.

def sawtooth_wave(freq0, amp0, num_pitches, sample_rate):
    freq = extend_pitch(freq0, num_pitches)

    mults = [-((-1) ** i) / (PI * i) for i in range(1, 1 + num_pitches)]
    amp = extend_pitch(amp0, mults)
    waveform = oscillator_bank(freq, amp, sample_rate=sample_rate)
    return freq, amp, waveform

Now synthesize a waveform

freq0 = torch.full((NUM_FRAMES, 1), F0)
amp0 = torch.ones((NUM_FRAMES, 1))
freq, amp, waveform = sawtooth_wave(freq0, amp0, int(SAMPLE_RATE / F0), SAMPLE_RATE)
plot(freq, amp, waveform, SAMPLE_RATE, zoom=(1 / F0, 3 / F0))

/pytorch/audio/src/torchaudio/prototype/functional/_dsp.py:63: UserWarning: Some frequencies are above nyquist frequency. Setting the corresponding amplitude to zero. This might cause numerically unstable gradient.
  warnings.warn(

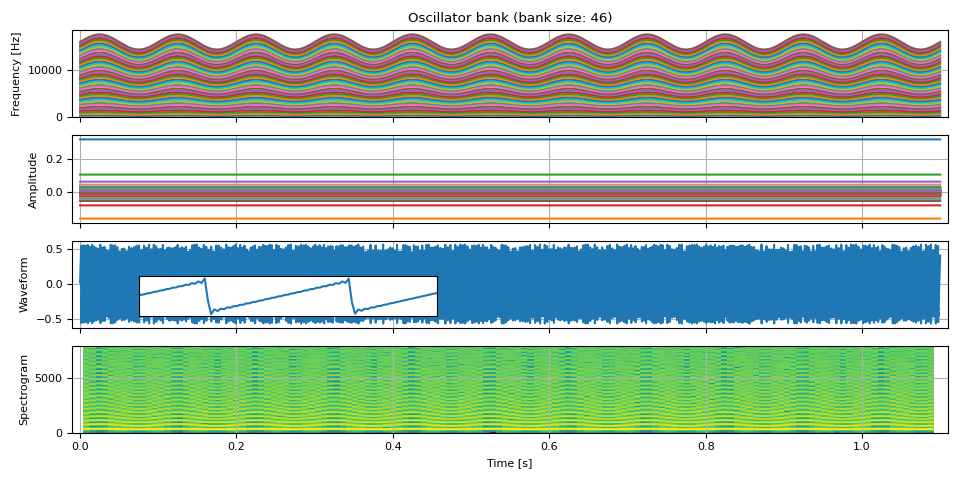
It is possible to oscillate the base frequency to create a time-varying tone based on sawtooth wave.

fm = 10  # rate at which the frequency oscillates [Hz]
f_dev = 0.1 * F0  # the degree of frequency oscillation [Hz]

phase = torch.linspace(0, fm * PI2 * DURATION, NUM_FRAMES)
freq0 = F0 + f_dev * torch.sin(phase).unsqueeze(-1)

freq, amp, waveform = sawtooth_wave(freq0, amp0, int(SAMPLE_RATE / F0), SAMPLE_RATE)
plot(freq, amp, waveform, SAMPLE_RATE, zoom=(1 / F0, 3 / F0))

/pytorch/audio/src/torchaudio/prototype/functional/_dsp.py:63: UserWarning: Some frequencies are above nyquist frequency. Setting the corresponding amplitude to zero. This might cause numerically unstable gradient.
  warnings.warn(

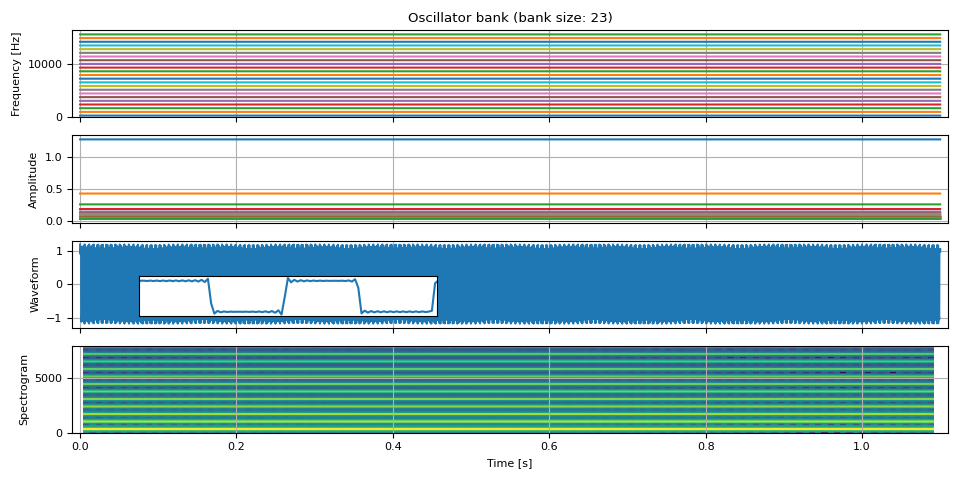
Square wave

Square wave contains only odd-integer harmonics.

\[\begin{align*} y_t &= \sum_{k=0}^{K-1} A_k \sin ( 2 \pi f_k t ) \\ \text{where} \\ f_k &= n f_0 \\ A_k &= \frac{ 4 }{n \pi} \\ n &= 2k + 1 \end{align*}\]

def square_wave(freq0, amp0, num_pitches, sample_rate):
    mults = [2.0 * i + 1.0 for i in range(num_pitches)]
    freq = extend_pitch(freq0, mults)

    mults = [4 / (PI * (2.0 * i + 1.0)) for i in range(num_pitches)]
    amp = extend_pitch(amp0, mults)

    waveform = oscillator_bank(freq, amp, sample_rate=sample_rate)
    return freq, amp, waveform

freq0 = torch.full((NUM_FRAMES, 1), F0)
amp0 = torch.ones((NUM_FRAMES, 1))
freq, amp, waveform = square_wave(freq0, amp0, int(SAMPLE_RATE / F0 / 2), SAMPLE_RATE)
plot(freq, amp, waveform, SAMPLE_RATE, zoom=(1 / F0, 3 / F0))

/pytorch/audio/src/torchaudio/prototype/functional/_dsp.py:63: UserWarning: Some frequencies are above nyquist frequency. Setting the corresponding amplitude to zero. This might cause numerically unstable gradient.
  warnings.warn(

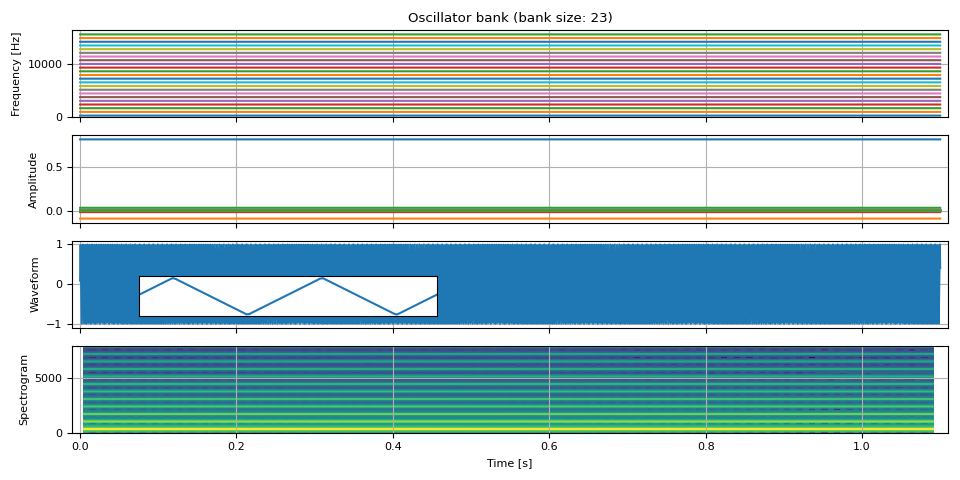
Triangle wave

Triangle wave also only contains odd-integer harmonics.

\[\begin{align*} y_t &= \sum_{k=0}^{K-1} A_k \sin ( 2 \pi f_k t ) \\ \text{where} \\ f_k &= n f_0 \\ A_k &= (-1) ^ k \frac{8}{(n\pi) ^ 2} \\ n &= 2k + 1 \end{align*}\]

def triangle_wave(freq0, amp0, num_pitches, sample_rate):
    mults = [2.0 * i + 1.0 for i in range(num_pitches)]
    freq = extend_pitch(freq0, mults)

    c = 8 / (PI**2)
    mults = [c * ((-1) ** i) / ((2.0 * i + 1.0) ** 2) for i in range(num_pitches)]
    amp = extend_pitch(amp0, mults)

    waveform = oscillator_bank(freq, amp, sample_rate=sample_rate)
    return freq, amp, waveform

freq, amp, waveform = triangle_wave(freq0, amp0, int(SAMPLE_RATE / F0 / 2), SAMPLE_RATE)
plot(freq, amp, waveform, SAMPLE_RATE, zoom=(1 / F0, 3 / F0))

/pytorch/audio/src/torchaudio/prototype/functional/_dsp.py:63: UserWarning: Some frequencies are above nyquist frequency. Setting the corresponding amplitude to zero. This might cause numerically unstable gradient.
  warnings.warn(

Inharmonic Paritials

Inharmonic partials refer to freqencies that are not integer multiple of fundamental frequency.

They are essential in re-creating realistic sound or making the result of synthesis more interesting.

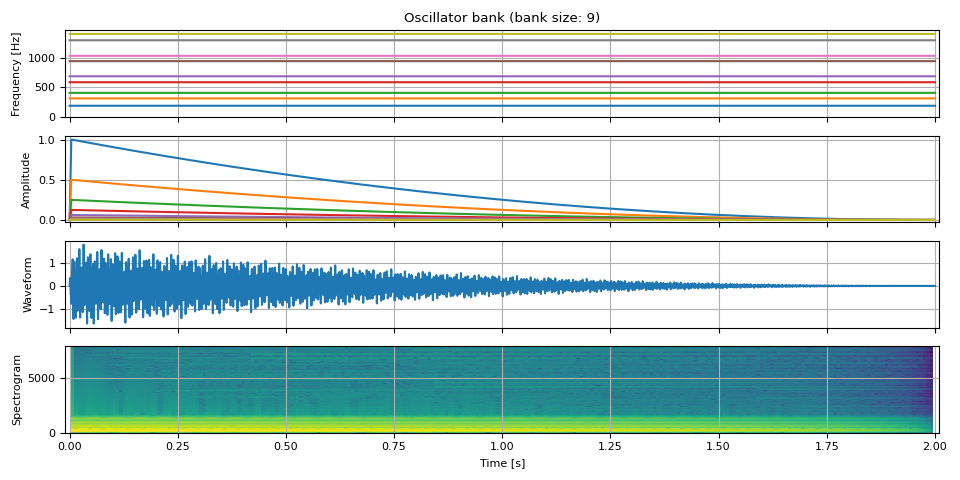
Bell sound

https://computermusicresource.com/Simple.bell.tutorial.html

num_tones = 9
duration = 2.0
num_frames = int(SAMPLE_RATE * duration)

freq0 = torch.full((num_frames, 1), F0)
mults = [0.56, 0.92, 1.19, 1.71, 2, 2.74, 3.0, 3.76, 4.07]
freq = extend_pitch(freq0, mults)

amp = adsr_envelope(
    num_frames=num_frames,
    attack=0.002,
    decay=0.998,
    sustain=0.0,
    release=0.0,
    n_decay=2,
)
amp = torch.stack([amp * (0.5**i) for i in range(num_tones)], dim=-1)

waveform = oscillator_bank(freq, amp, sample_rate=SAMPLE_RATE)

plot(freq, amp, waveform, SAMPLE_RATE, vol=0.4)

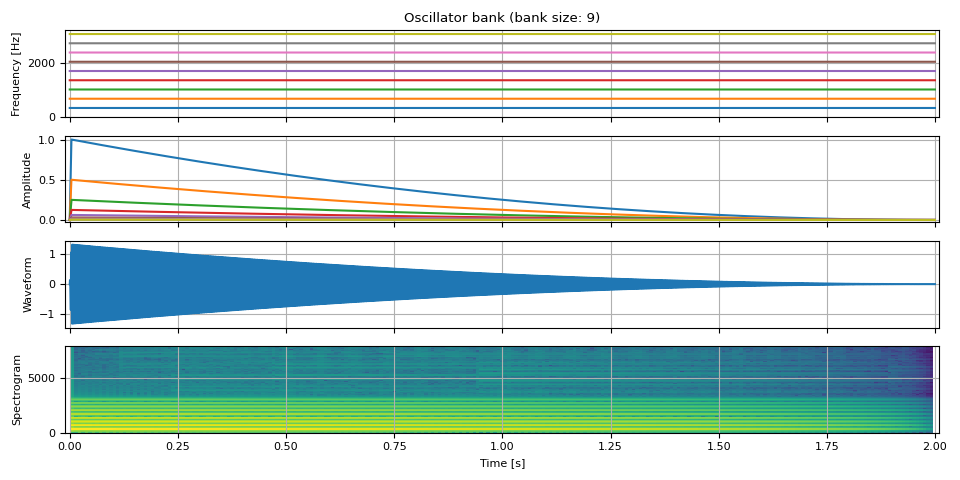
As a comparison, the following is the harmonic version of the above. Only frequency values are different. The number of overtones and its amplitudes are same.

freq = extend_pitch(freq0, num_tones)
waveform = oscillator_bank(freq, amp, sample_rate=SAMPLE_RATE)

plot(freq, amp, waveform, SAMPLE_RATE)

References

• https://en.wikipedia.org/wiki/Additive_synthesis

• https://computermusicresource.com/Simple.bell.tutorial.html

• https://computermusicresource.com/Definitions/additive.synthesis.html