torchaudio.transforms
torchaudio.transforms module contains common audio processings and feature extractions. The following diagram shows the relationship between some of the available transforms.
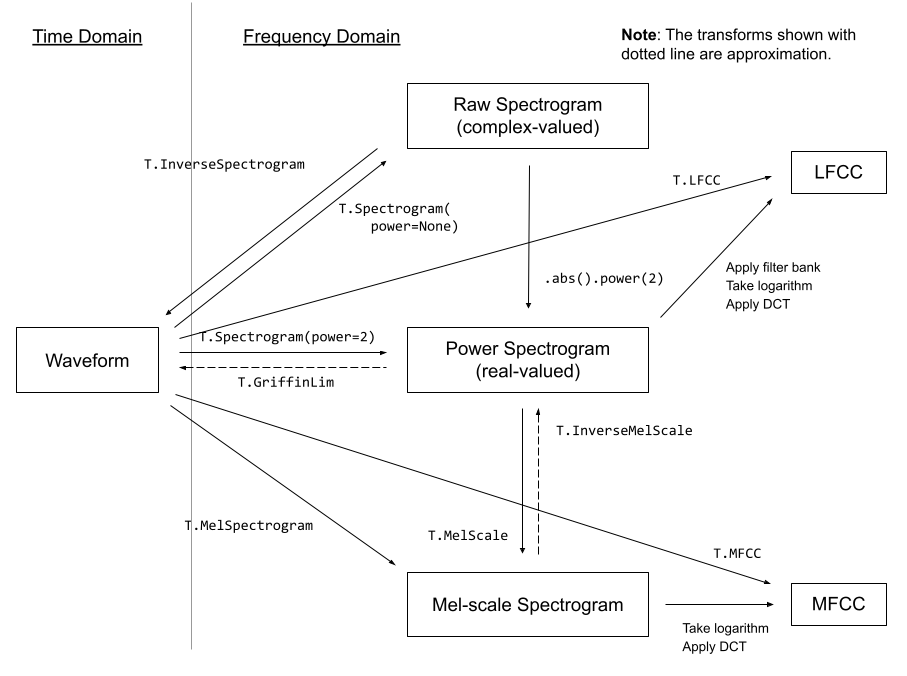
Transforms are implemented using torch.nn.Module. Common ways to build a processing pipeline are to define custom Module class or chain Modules together using torch.nn.Sequential, then move it to a target device and data type.
# Define custom feature extraction pipeline.
#
# 1. Resample audio
# 2. Convert to power spectrogram
# 3. Apply augmentations
# 4. Convert to mel-scale
#
class MyPipeline(torch.nn.Module):
def __init__(
self,
input_freq=16000,
resample_freq=8000,
n_fft=1024,
n_mel=256,
stretch_factor=0.8,
):
super().__init__()
self.resample = Resample(orig_freq=input_freq, new_freq=resample_freq)
self.spec = Spectrogram(n_fft=n_fft, power=2)
self.spec_aug = torch.nn.Sequential(
TimeStretch(stretch_factor, fixed_rate=True),
FrequencyMasking(freq_mask_param=80),
TimeMasking(time_mask_param=80),
)
self.mel_scale = MelScale(
n_mels=n_mel, sample_rate=resample_freq, n_stft=n_fft // 2 + 1)
def forward(self, waveform: torch.Tensor) -> torch.Tensor:
# Resample the input
resampled = self.resample(waveform)
# Convert to power spectrogram
spec = self.spec(resampled)
# Apply SpecAugment
spec = self.spec_aug(spec)
# Convert to mel-scale
mel = self.mel_scale(spec)
return mel
# Instantiate a pipeline
pipeline = MyPipeline()
# Move the computation graph to CUDA
pipeline.to(device=torch.device("cuda"), dtype=torch.float32)
# Perform the transform
features = pipeline(waveform)
Please check out tutorials that cover in-depth usage of trasforms.
Utility
Turn a tensor from the power/amplitude scale to the decibel scale. |
|
Encode signal based on mu-law companding. |
|
Decode mu-law encoded signal. |
|
Resample a signal from one frequency to another. |
|
Add a fade in and/or fade out to an waveform. |
|
Adjust volume of waveform. |
|
Measure audio loudness according to the ITU-R BS.1770-4 recommendation. |
|
Scales and adds noise to waveform per signal-to-noise ratio. |
|
Convolves inputs along their last dimension using the direct method. |
|
Convolves inputs along their last dimension using FFT. |
|
Adjusts waveform speed. |
|
Applies the speed perturbation augmentation introduced in Audio augmentation for speech recognition [Ko et al., 2015]. |
|
De-emphasizes a waveform along its last dimension. |
|
Pre-emphasizes a waveform along its last dimension. |
Feature Extractions
Create a spectrogram from a audio signal. |
|
Create an inverse spectrogram to recover an audio signal from a spectrogram. |
|
Turn a normal STFT into a mel frequency STFT with triangular filter banks. |
|
Estimate a STFT in normal frequency domain from mel frequency domain. |
|
Create MelSpectrogram for a raw audio signal. |
|
Compute waveform from a linear scale magnitude spectrogram using the Griffin-Lim transformation. |
|
Create the Mel-frequency cepstrum coefficients from an audio signal. |
|
Create the linear-frequency cepstrum coefficients from an audio signal. |
|
Compute delta coefficients of a tensor, usually a spectrogram. |
|
Shift the pitch of a waveform by |
|
Apply sliding-window cepstral mean (and optionally variance) normalization per utterance. |
|
Compute the spectral centroid for each channel along the time axis. |
|
Voice Activity Detector. |
Augmentations
The following transforms implement popular augmentation techniques known as SpecAugment [Park et al., 2019].
Apply masking to a spectrogram in the frequency domain. |
|
Apply masking to a spectrogram in the time domain. |
|
Stretch stft in time without modifying pitch for a given rate. |
Loss
Compute the RNN Transducer loss from Sequence Transduction with Recurrent Neural Networks [Graves, 2012]. |
Multi-channel
Compute cross-channel power spectral density (PSD) matrix. |
|
Minimum Variance Distortionless Response (MVDR) module that performs MVDR beamforming with Time-Frequency masks. |
|
Minimum Variance Distortionless Response (MVDR [Capon, 1969]) module based on the relative transfer function (RTF) and power spectral density (PSD) matrix of noise. |
|
Minimum Variance Distortionless Response (MVDR [Capon, 1969]) module based on the method proposed by Souden et, al. [Souden et al., 2009]. |