PyTorch DDP has been widely adopted across the industry for distributed training, which by default runs synchronous SGD to synchronize gradients across model replicas at every step. The performance of this technique is critical for fast iteration during model exploration as well as resource and cost saving. The performance is critical for fast iteration and cost saving of model development and exploration. To resolve a ubiquitous performance bottleneck introduced by slow nodes in large-scale training, Cruise and Meta co-developed a solution based on the Hierarchical SGD algorithm to significantly accelerate training in the presence of these stragglers.
The Need For Straggler Mitigation
In DDP setup, a straggler problem can occur when one or more processes run much slower (“stragglers”) than other processes. When this happens, all the processes have to wait for the stragglers before synchronizing gradients and completing the communication, which essentially bottlenecks distributed performance to the slowest worker.As a result, even for the cases of training relatively small models, the communication cost can still be a major performance bottleneck.
Potential Causes of Stragglers
Severe straggler issues are usually caused by workload imbalance before synchronization, and many factors can contribute to this imbalance. For instance, some data loader workers in the distributed environment can become stragglers, because some input examples can be outliers in terms of the data size, or the data transfer of some examples can be drastically slowed down due to unstable network I/O, or the on-the-fly data transformation costs can have a high variance.
Besides data loading, other phases before gradient synchronization can also cause stragglers, such as unbalanced workloads of embedding table lookup during the forward pass in recommendation systems.
The Appearance of Stragglers
If we profile DDP training jobs that have stragglers, we can find that some processes may have much higher gradient synchronization costs (a.k.a., allreducing gradients) than other processes at a certain step. As a result, the distributed performance can be dominated by the communication cost even if the model size is very small. In this case, some processes run faster than the straggler(s) at a step, and hence they have to wait for the stragglers and spend a much longer time on allreduce.
The below shows screenshots of two trace files output by PyTorch profiler in a use case. Each screenshot profiles 3 steps.
- The first screenshot shows that a process has a very high allreduce cost in both the first and the third steps, because this process reaches the synchronization phase earlier than the straggler(s), and it spends more time on waiting. On the other hand, the allreduce cost is relatively small in the second step, this suggests that 1) there is no straggler at this step; or 2) this process is the straggler among all the processes, so it does not need to wait for any other process.
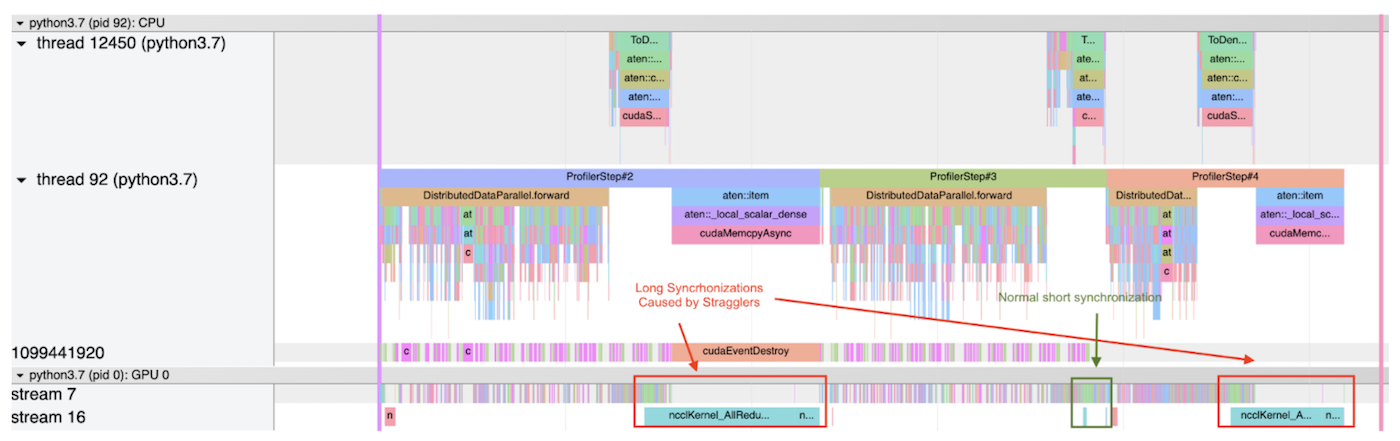
Both the 1st and the 3rd Steps Are Slowed Down by Stragglers
- The second screenshot shows a normal case without stragglers. In this case, all the gradient synchronizations are relatively short.
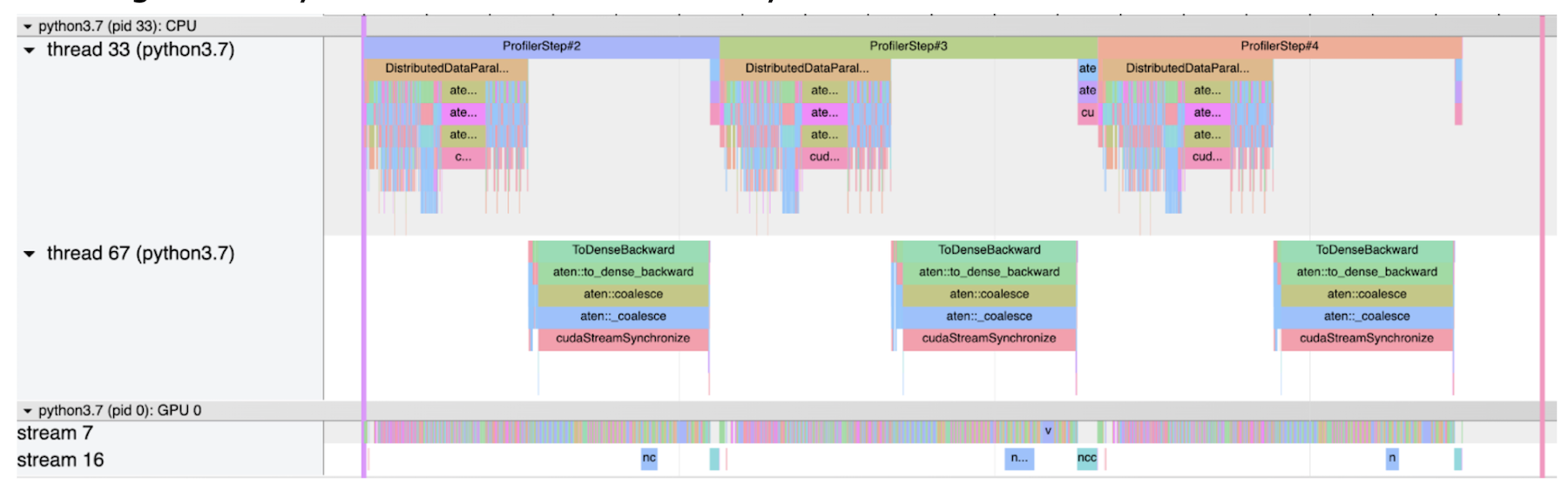
Normal Case Without Stragglers
Hierarchical SGD in PyTorch
Recently hierarchical SGD has been proposed to optimize the communication costs by mainly reducing the total amount of data transfer in large-scale distributed training, and multiple convergence analyses have been provided (example). As a main novelty of this post, at Cruise we could leverage hierarchical SGD to mitigate stragglers, which may also occur on training relatively small models. Our implementation has been upstreamed by Cruise to PyTorch in early 2022.
How Does Hierarchical SGD Work?
As the name implies, hierarchical SGD organizes all the processes into groups at different levels as a hierarchy, and runs synchronization by following the rules below:
- All the groups at the same level have the same number of processes, and the processes in these groups synchronize at the same frequency concurrently, where the synchronization period is pre-defined by the user.
- The higher level a group is, the larger synchronization period is used, as the synchronization becomes more expensive.
- When multiple overlapping groups are supposed to synchronize according to their periods, to reduce redundant synchronization and avoid data race across groups, only the highest-level group runs synchronization.
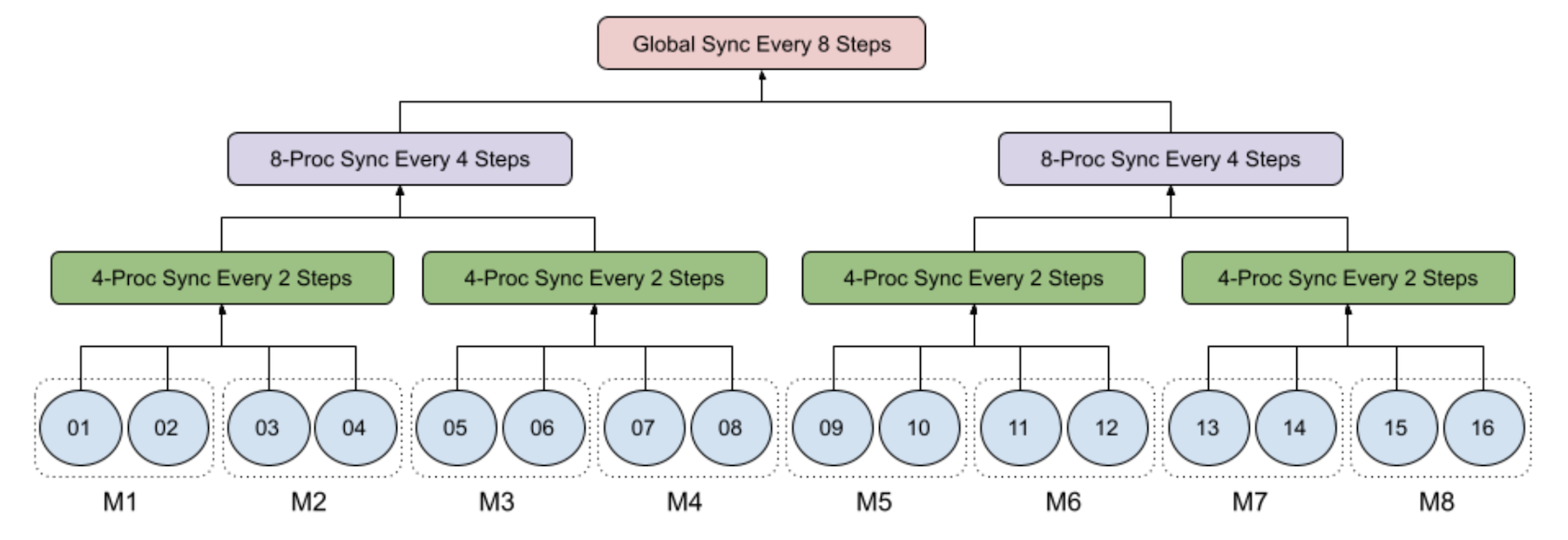
The following figure illustrates an example of 4-level hierarchy SGD among 16 processes on 8 machines, each of which has 2 GPUs:
- Level 1: Each process runs mini-batch SGD locally;
- Level 2: Each 4-process group across 2 machines runs synchronization every 2 steps;
- Level 3: Each 8-process group across 4 machines runs synchronization every 4 steps;
- Level 4: The global process group of all 16 processes over 8 machines runs synchronization every 8 steps.
Particularly, when the step number can be divided by 8, only the synchronization at 3) is executed, and when the step number can be divided by 4 but not 8, only the synchronization at 2) is executed.
Intuitively, hierarchical SGD can be viewed as an extension of local SGD, which only has a two-level hierarchy – every process runs mini-batch SGD locally and then synchronizes globally at a certain frequency. This can also help explain that, just like local SGD, hierarchical SGD synchronizes model parameters instead of gradients. Otherwise the gradient descent will be mathematically incorrect when the frequency is greater than 1.
Why Can Hierarchical SGD Mitigate Stragglers?
The key insight here is that, when there is a random straggler, it only directly slows down a relatively small group of processes instead of all the processes. Next time another random straggler is very likely to slow down a different small group, and hence a hierarchy can help smooth out the straggler effect.
The example below assumes that there is a random straggler among totally 8 processes at every step. After 4 steps, vanilla DDP that runs synchronous SGD will be slowed down by straggler 4 times, because it runs global synchronization at every step. In contrast, hierarchical SGD runs synchronization with the groups of 4 processes after the first two steps, and then a global synchronization after another two steps. We can see that both the first two and the last two stragglers have a large overlap, and hence the performance loss can be mitigated.
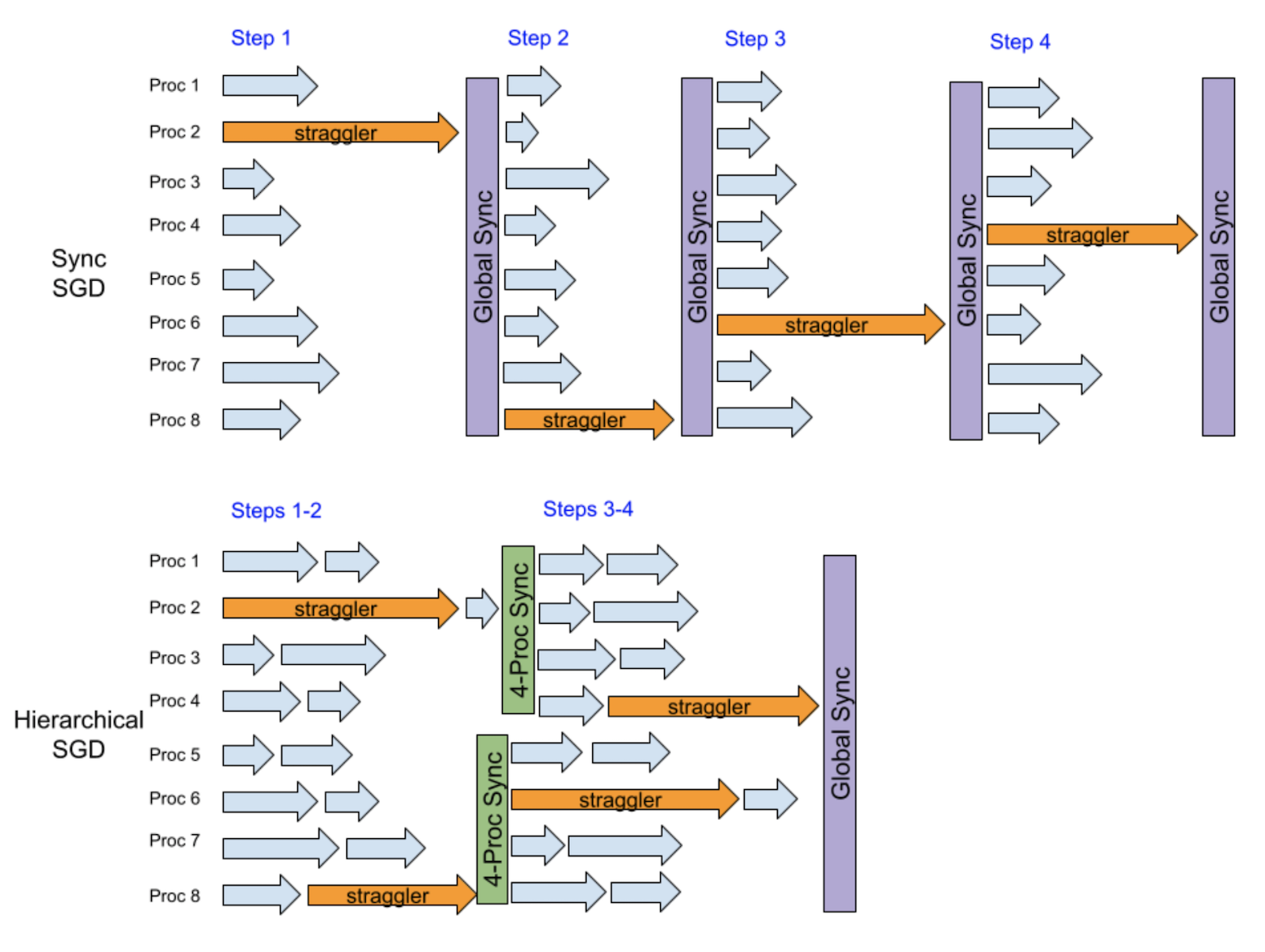
Essentially, the mitigation effect of this hierarchical SGD example actually is between local SGD at a frequency of every 2 steps and every 4 steps. The main advantage of hierarchical SGD over local SGD is a better convergence efficiency of the same global synchronization frequency, because hierarchical SGD allows more low-level synchronization. Moreover, it is possible for hierarchical SGD to provide a global synchronization frequency lower than local SGD with model parity, leading to a higher training performance, especially in a large-scale distributed training.
Ease of Use
Straggler mitigation is not a novel study in distributed training. Multiple approaches have been proposed, such as gossip SGD, data encoding, gradient coding, as well as some particularly designed for parameter-server architecture, including backup workers and stale synchronous parallel. However, to the best of our knowledge, before this effort we have not found a good open-source PyTorch implementation of straggler mitigation that can work like a plugin to our training system at Cruise. In contrast, our implementation only requires the minimal changes – no need to modify the existing code or tune any existing hyperparameters. This is a very appealing advantage for industry users.
As the code example below shows, only a few lines need to be added to the setup of DDP model, and the training loop code can keep untouched. As explained previously, hierarchical SGD is an extended form of local SGD, so the enablement can be quite similar to local SGD (see PyTorch docs of PostLocalSGDOptimizer):
- Register a post-local SGD communication hook to run a warmup stage of fully synchronous SGD and defer hierarchical SGD.
- Create a post-local SGD optimizer that wraps an existing local optimizer and a hierarchical SGD configuration.
import torch.distributed.algorithms.model_averaging.hierarchical_model_averager as hierarchicalSGD
from torch.distributed.algorithms.ddp_comm_hooks.post_localSGD_hook import (
PostLocalSGDState,
post_localSGD_hook,
)
from torch.distributed.optim import PostLocalSGDOptimizer
ddp_model = nn.parallel.DistributedDataParallel(
module=model,
device_ids=[rank],
)
# Register a post-local SGD communication hook for the warmup.
subgroup, _ = torch.distributed.new_subgroups()
state = PostLocalSGDState(subgroup=subgroup, start_localSGD_iter=1_000)
ddp_model.register_comm_hook(state, post_localSGD_hook)
# Wraps the existing (local) optimizer to run hierarchical model averaging.
optim = PostLocalSGDOptimizer(
optim=optim,
averager=hierarchicalSGD.HierarchicalModelAverager(
# The config runs a 4-level hierarchy SGD among 128 processes:
# 1) Each process runs mini-batch SGD locally;
# 2) Each 8-process group synchronize every 2 steps;
# 3) Each 32-process group synchronize every 4 steps;
# 4) All 128 processes synchronize every 8 steps.
period_group_size_dict=OrderedDict([(2, 8), (4, 32), (8, 128)]),
# Do not run hierarchical SGD until 1K steps for model parity.
warmup_steps=1_000)
)
Algorithm Hyperparameters
Hierarchical SGD has two major hyperparameters: period_group_size_dict and warmup_steps.
- period_group_size_dict is an ordered dictionary mapping from synchronization period to process group size, used for initializing process groups of different sizes in a hierarchy to synchronize parameters concurrently. A larger group is expected to use a larger synchronization period.
- warmup_steps specifies a number of steps as the warmup stage to run synchronous SGD before hierarchical SGD. Similar to post-local SGD algorithm, a warmup stage is usually recommended to achieve a higher accuracy. The value should be the same as start_localSGD_iter arg used in PostLocalSGDState when post_localSGD_hook is registered. Typically the warmup stage should at least cover the beginning of training when the loss is decreased drastically.
A subtle difference between the PyTorch implementation and the initial design proposed by relevant papers is that, after the warmup stage, by default the processes within each host still run intra-host gradient synchronization at every step. This is because that:
- The intra-host communication is relatively cheap, and it can usually significantly accelerate the convergence;
- The intra-host group (of size 4 or 8 for most industry users) can usually be a good choice of the smallest group of processes that synchronize most frequently in hierarchical SGD. If the synchronization period is 1, then gradient synchronization is faster than model parameter synchronization (a.k.a., model averaging), because DDP automatically overlaps gradient synchronization and the backward pass.
Such intra-host gradient synchronization can be disabled by unsetting post_local_gradient_allreduce arg in PostLocalSGDState.
Demonstration
Now we demonstrate that hierarchical SGD can accelerate distributed training by mitigating stragglers.
Experimental Setup
We compared the performance of hierarchical SGD against local SGD and synchronous SGD on ResNet18 (model size: 45MB). Since the model is so small, the training is not bottlenecked by data transfer cost during synchronization. To avoid the noises incurred by data loading from remote storage, the input data was randomly simulated from memory. We varied the number of GPUs used by training from 64 to 256. The batch size per worker is 32, and the number of iterations of training is 1,000. Since we don’t evaluate convergence efficiency in this set of experiments, warmup is not enabled.
We also emulated stragglers at a rate of 1% on 128 and 256 GPUs, and 2% on 64 GPUs, to make sure at least one stragglers at every step on average. These stragglers randomly appear on different CUDA devices. Each straggler stalls for 1 second besides the normal per-step training time (~55ms in our setup). This can be perceived as a practical scenario where 1% or 2% of input data are outliers in terms of the data pre-processing cost (I/O and/or data transformation on the fly) during training, and such cost is 20X+ larger than the average.
The code snippet below shows how a straggler can be emulated in the training loop. We applied it to a ResNet model, and it can be easily applied to the other models as well.
loss = loss_fn(y_pred, y)
# Emulate a straggler that lags for 1 second at a rate of 1%.
if random.randint(1, 100) == 1:
time.sleep(1)
loss.backward()
optimizer.step()
The experiments are conducted on us-central1 GCP cluster. Each machine has 4 NVIDIA Tesla T4 GPUs with 16 GB memory per GPU, connected through a 32 Gbit/s ethernet network. Each instance also features 96 vCPUs, 360 GB RAM.
| Architecture | ResNet18 (45MB) |
| Workers | 64, 128, 256 |
| Backend | NCCL |
| GPU | Tesla T4, 16 GB memory |
| Batch size | 32 x ## of workers |
| Straggler Duration | 1 sec |
| Straggler Rate | 1% on 128 and 256 GPUs, 2% on 64 GPUs |
We used multiple configurations for both local SGD and hierarchical SGD. Local SGD runs global synchronization every 2, 4, and 8 steps, respectively.
We ran hierarchical SGD with the following configurations:
- On 64 GPUs:
- Each 8-process group, 32-process, and the global 64-process group synchronizes every 2, 4, and 8 steps, respectively. Denoted as “HSGD 2-8,4-32,8-64”.
- Each 32-process group and the global 64-process group synchronizes every 4 and 8 steps, respectively. Denoted as “HSGD 4-32,8-64”.
- On 128 GPUs:
- Each 8-process group, 32-process group, and the global 128-process group synchronizes every 2, 4, and 8 steps, respectively. Denoted as “HSGD 2-8,4-32,8-128”.
- Each 32-process group and the global 128-process group synchronizes every 4 and 8 steps, respectively. Denoted as “HSGD 4-32,8-128”.
- On 256 GPUs:
- Each 4-process group, 16-process group, 64-process group, and the global 256-process group synchronizes every 1, 2, 4, and 8 steps, respectively. Denoted as “HSGD 1-4,2-16,4-64,8-256”.
- Each 8-process group, 64-process group, and the global 256-process group synchronizes every 2, 4, and 8 steps. Denoted as “HSGD 2-8,4-64,8-256”.
- Each 16-process group and the global 256-process group synchronizes every 4 and 8 steps, respectively. Denoted as “HSGD 4-16,8-256”.
Experimental Results
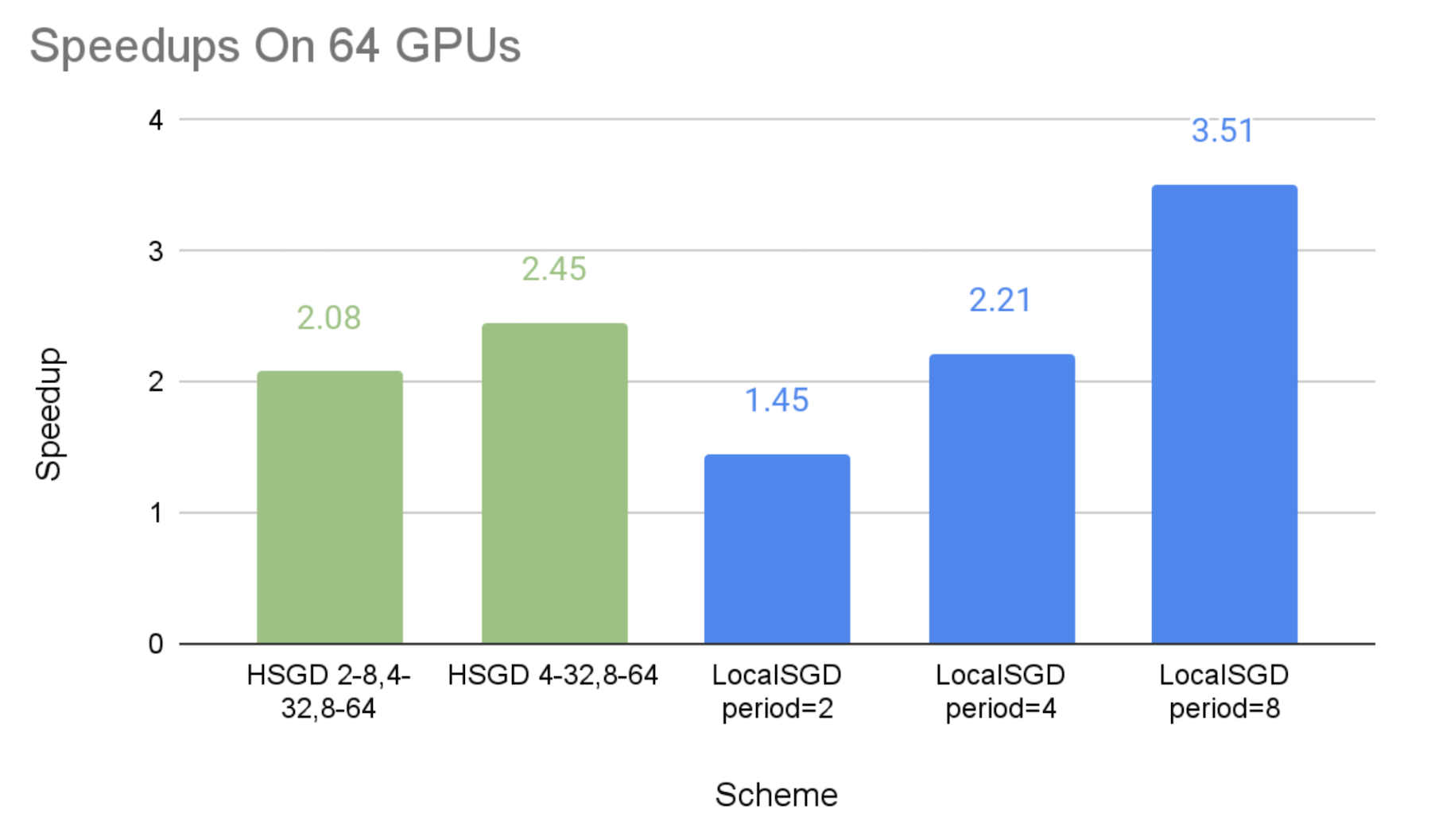
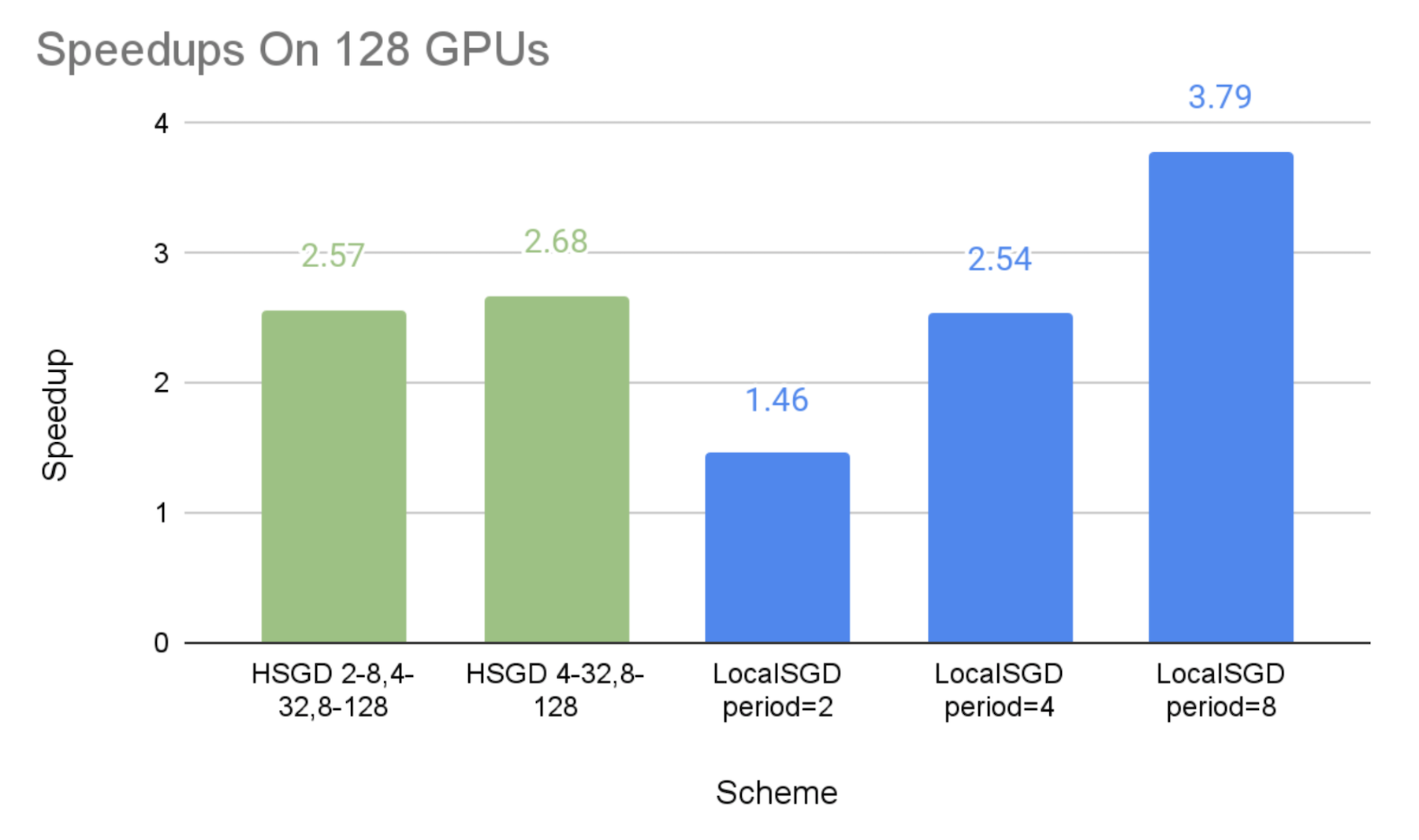
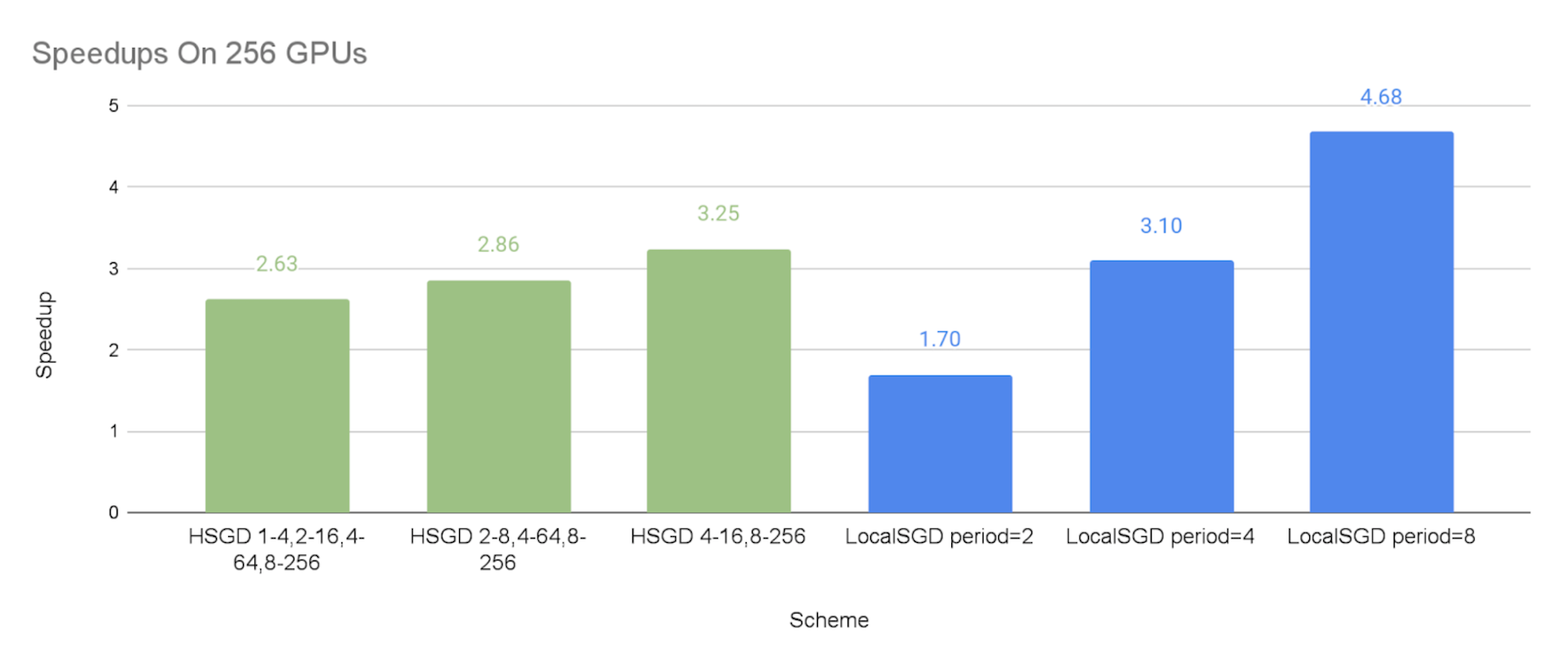
The figures below show the speedups of different communication schemes against the baseline of synchronous SGD, with the emulated stragglers. We can make the following observations:
- As expected, we can see that both hierarchical SGD and local SGD can achieve a higher speedup with a lower synchronization frequency.
- The speedups of the hierarchical SGD schemes are 2.08X-2.45X on 64 GPUs, 2.57X-2.68X on 128 GPUs, and 2.63X-3.25X on 256 GPUs, respectively. This shows that hierarchical SGD can significantly mitigate stragglers, and such mitigation can be more effective at a larger scale.
- The performance of local SGD with the synchronization period of 2 steps and 8 steps can be perceived as the lower bound and upper bound of the experimented hierarchical SGD schemes, respectively. This is because the hierarchical SGD schemes synchronize less frequently than every 2 steps globally, but their low-level synchronization at small groups are the extra overheads in comparison with the global synchronization every 8 steps.
Overall, hierarchical SGD can provide a finer-grained trade-off between communication cost and model quality than local SGD. Therefore, when local SGD at a relatively large synchronization period like 8 or 4 cannot give a satisfactory convergence efficiency, hierarchical SGD can have a much better chance to achieve both a good speedup and a model parity.
Since only simulated data is used in the experiments, we did not demonstrate the model parity here, which in practice can be achieved in two ways:
- Tuning the hyperparameters including both hierarchy and warmup steps;
- For some cases, hierarchical SGD could lead to a slightly lower quality than the original model for the same number of training steps (i.e., lower convergence rate), but with a speedup like 2X+ per training step, it is still possible to achieve model parity with more steps but still less total training time.
Limitations
Before applying hierarchical SGD to straggler mitigation, the user should be aware of a few limitations of this approach:
- This approach can only mitigate non-persistent stragglers, which occur to different workers at different times. However, for the case of persistent stragglers, which can be caused by hardware degradation or a network issue on a specific host, these stragglers will slow down the same low-level subgroup at every time, leading to nearly no straggler mitigation.
- This approach can only mitigate low-frequency stragglers. E.g., if 30% workers can randomly become stragglers at every step, then most low-level synchronizations will still be slowed down by stragglers. As a result, hierarchical SGD may not show an obvious performance advantage over synchronous SGD.
- Since hierarchical SGD applies model averaging that does not overlap with backward like gradient averaging used by vanilla DDP, its performance gain of straggler mitigation must outweigh the performance loss of no overlap between communication and backward pass. Therefore, if stragglers only slow down training by less than 10%, hierarchical SGD may not be able to bring much speedup. This limitation can be addressed by overlapping optimizer step and backward pass in the future.
- Since hierarchical SGD is less well-studied than local SGD, there is no guarantee that hierarchical SGD with a finer-grained synchronization granularity can converge faster than certain advanced forms of local SGD, such as SlowMo, which can improve convergence efficiency with slow momentum. However, to the best of our knowledge, these advanced algorithms cannot be natively supported as a PyTorch DDP plugin like hierarchical SGD yet.
Acknowledgements
We would like to thank Cruise teammates Bo Tian, Sergei Vorobev, Eugene Selivonchyk, Tsugn-Hsien Lee, Dan Ring, Ian Ackerman, Lei Chen, Maegan Chew, Viet Anh To, Xiaohui Long, Zeyu Chen, Alexander Sidorov, Igor Tsvetkov, Xin Hu, Manav Kataria, Marina Rubtsova, and Mohamed Fawzy, as well as Meta teammates Shen Li, Yanli Zhao, Suraj Subramanian, Hamid Shojanzeri, Anjali Sridhar and Bernard Nguyen for the support.
