import torch
model = torch.hub.load('pytorch/vision:v0.10.0', 'shufflenet_v2_x1_0', pretrained=True)
model.eval()
All pre-trained models expect input images normalized in the same way,
i.e. mini-batches of 3-channel RGB images of shape (3 x H x W), where H and W are expected to be at least 224.
The images have to be loaded in to a range of [0, 1] and then normalized using mean = [0.485, 0.456, 0.406]
and std = [0.229, 0.224, 0.225].
Here’s a sample execution.
# Download an example image from the pytorch website
import urllib
url, filename = ("https://github.com/pytorch/hub/raw/master/images/dog.jpg", "dog.jpg")
try: urllib.URLopener().retrieve(url, filename)
except: urllib.request.urlretrieve(url, filename)
# sample execution (requires torchvision)
from PIL import Image
from torchvision import transforms
input_image = Image.open(filename)
preprocess = transforms.Compose([
transforms.Resize(256),
transforms.CenterCrop(224),
transforms.ToTensor(),
transforms.Normalize(mean=[0.485, 0.456, 0.406], std=[0.229, 0.224, 0.225]),
])
input_tensor = preprocess(input_image)
input_batch = input_tensor.unsqueeze(0) # create a mini-batch as expected by the model
# move the input and model to GPU for speed if available
if torch.cuda.is_available():
input_batch = input_batch.to('cuda')
model.to('cuda')
with torch.no_grad():
output = model(input_batch)
# Tensor of shape 1000, with confidence scores over ImageNet's 1000 classes
print(output[0])
# The output has unnormalized scores. To get probabilities, you can run a softmax on it.
probabilities = torch.nn.functional.softmax(output[0], dim=0)
print(probabilities)
# Download ImageNet labels
!wget https://raw.githubusercontent.com/pytorch/hub/master/imagenet_classes.txt
# Read the categories
with open("imagenet_classes.txt", "r") as f:
categories = [s.strip() for s in f.readlines()]
# Show top categories per image
top5_prob, top5_catid = torch.topk(probabilities, 5)
for i in range(top5_prob.size(0)):
print(categories[top5_catid[i]], top5_prob[i].item())
Model Description
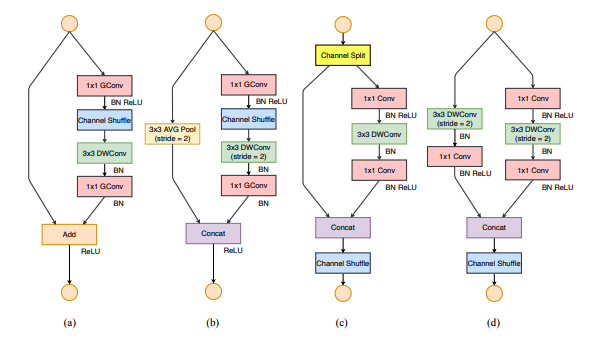
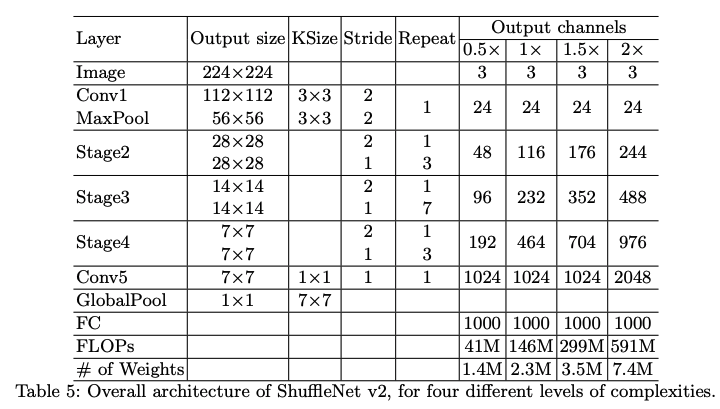
Previously, neural network architecture design was mostly guided by the indirect metric of computation complexity, i.e., FLOPs. However, the direct metric, e.g., speed, also depends on the other factors such as memory access cost and platform characteristics. Based on a series of controlled experiments, this work derives several practical guidelines for efficient network design. Accordingly, a new architecture is presented, called ShuffleNet V2. Comprehensive ablation experiments verify that our model is the state of-the-art in terms of speed and accuracy tradeoff.
| Model structure | Top-1 error | Top-5 error |
|---|---|---|
| shufflenet_v2 | 30.64 | 11.68 |