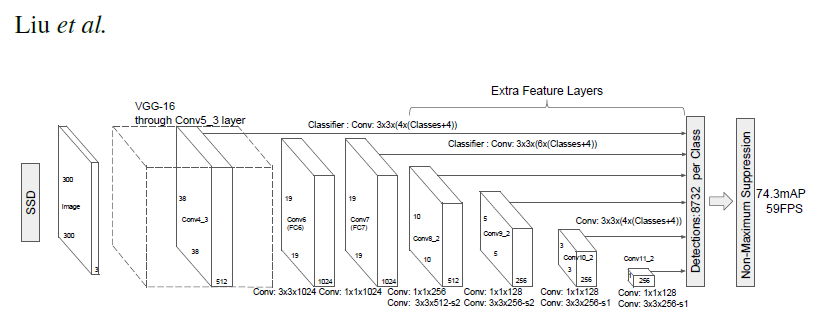
Model Description
This SSD300 model is based on the SSD: Single Shot MultiBox Detector paper, which describes SSD as “a method for detecting objects in images using a single deep neural network”. The input size is fixed to 300x300.
The main difference between this model and the one described in the paper is in the backbone. Specifically, the VGG model is obsolete and is replaced by the ResNet-50 model.
From the Speed/accuracy trade-offs for modern convolutional object detectors paper, the following enhancements were made to the backbone:
- The conv5_x, avgpool, fc and softmax layers were removed from the original classification model.
- All strides in conv4_x are set to 1x1.
The backbone is followed by 5 additional convolutional layers. In addition to the convolutional layers, we attached 6 detection heads:
- The first detection head is attached to the last conv4_x layer.
- The other five detection heads are attached to the corresponding 5 additional layers.
Detector heads are similar to the ones referenced in the paper, however, they are enhanced by additional BatchNorm layers after each convolution.
Example
In the example below we will use the pretrained SSD model to detect objects in sample images and visualize the result.
To run the example you need some extra python packages installed. These are needed for preprocessing images and visualization.
pip install numpy scipy scikit-image matplotlib
Load an SSD model pretrained on COCO dataset, as well as a set of utility methods for convenient and comprehensive formatting of input and output of the model.
import torch
ssd_model = torch.hub.load('NVIDIA/DeepLearningExamples:torchhub', 'nvidia_ssd')
utils = torch.hub.load('NVIDIA/DeepLearningExamples:torchhub', 'nvidia_ssd_processing_utils')
Now, prepare the loaded model for inference
ssd_model.to('cuda')
ssd_model.eval()
Prepare input images for object detection. (Example links below correspond to first few test images from the COCO dataset, but you can also specify paths to your local images here)
uris = [
'http://images.cocodataset.org/val2017/000000397133.jpg',
'http://images.cocodataset.org/val2017/000000037777.jpg',
'http://images.cocodataset.org/val2017/000000252219.jpg'
]
Format the images to comply with the network input and convert them to tensor.
inputs = [utils.prepare_input(uri) for uri in uris]
tensor = utils.prepare_tensor(inputs)
Run the SSD network to perform object detection.
with torch.no_grad():
detections_batch = ssd_model(tensor)
By default, raw output from SSD network per input image contains 8732 boxes with localization and class probability distribution. Let’s filter this output to only get reasonable detections (confidence>40%) in a more comprehensive format.
results_per_input = utils.decode_results(detections_batch)
best_results_per_input = [utils.pick_best(results, 0.40) for results in results_per_input]
The model was trained on COCO dataset, which we need to access in order to translate class IDs into object names. For the first time, downloading annotations may take a while.
classes_to_labels = utils.get_coco_object_dictionary()
Finally, let’s visualize our detections
from matplotlib import pyplot as plt
import matplotlib.patches as patches
for image_idx in range(len(best_results_per_input)):
fig, ax = plt.subplots(1)
# Show original, denormalized image...
image = inputs[image_idx] / 2 + 0.5
ax.imshow(image)
# ...with detections
bboxes, classes, confidences = best_results_per_input[image_idx]
for idx in range(len(bboxes)):
left, bot, right, top = bboxes[idx]
x, y, w, h = [val * 300 for val in [left, bot, right - left, top - bot]]
rect = patches.Rectangle((x, y), w, h, linewidth=1, edgecolor='r', facecolor='none')
ax.add_patch(rect)
ax.text(x, y, "{} {:.0f}%".format(classes_to_labels[classes[idx] - 1], confidences[idx]*100), bbox=dict(facecolor='white', alpha=0.5))
plt.show()
Details
For detailed information on model input and output, training recipies, inference and performance visit: github and/or NGC
References
- SSD: Single Shot MultiBox Detector paper
- Speed/accuracy trade-offs for modern convolutional object detectors paper
- SSD on NGC
- SSD on github