IBM: Krish Agarwal, Rishi Astra, Adnan Hoque, Mudhakar Srivatsa, Raghu Ganti
Meta: Less Wright, Sijia Chen
Quantization is a method for improving model inference speeds by compressing model weights and performing (faster) computation in lower precision data types. However, quantization can result in accuracy loss due to the presence of outliers. Recent works like QuaRot, SpinQuant, and FlashAttention-3 introduce methods to increase the numerical accuracy of INT4, INT8 and FP8 quantization in LLMs. These methods rely on Hadamard Transforms. In this blog, we present HadaCore, a Hadamard Transform CUDA kernel that achieves state-of-the-art performance on NVIDIA A100 and H100 GPUs. Our kernel achieves speedups of 1.1–1.4x and 1.0–1.3x, with a peak gain of 3.5x and 3.6x respectively, over Dao AI Lab’s Fast Hadamard Transform Kernel. We leverage a hardware-aware work decomposition that benefits from Tensor Core acceleration while maintaining quantization error reduction.
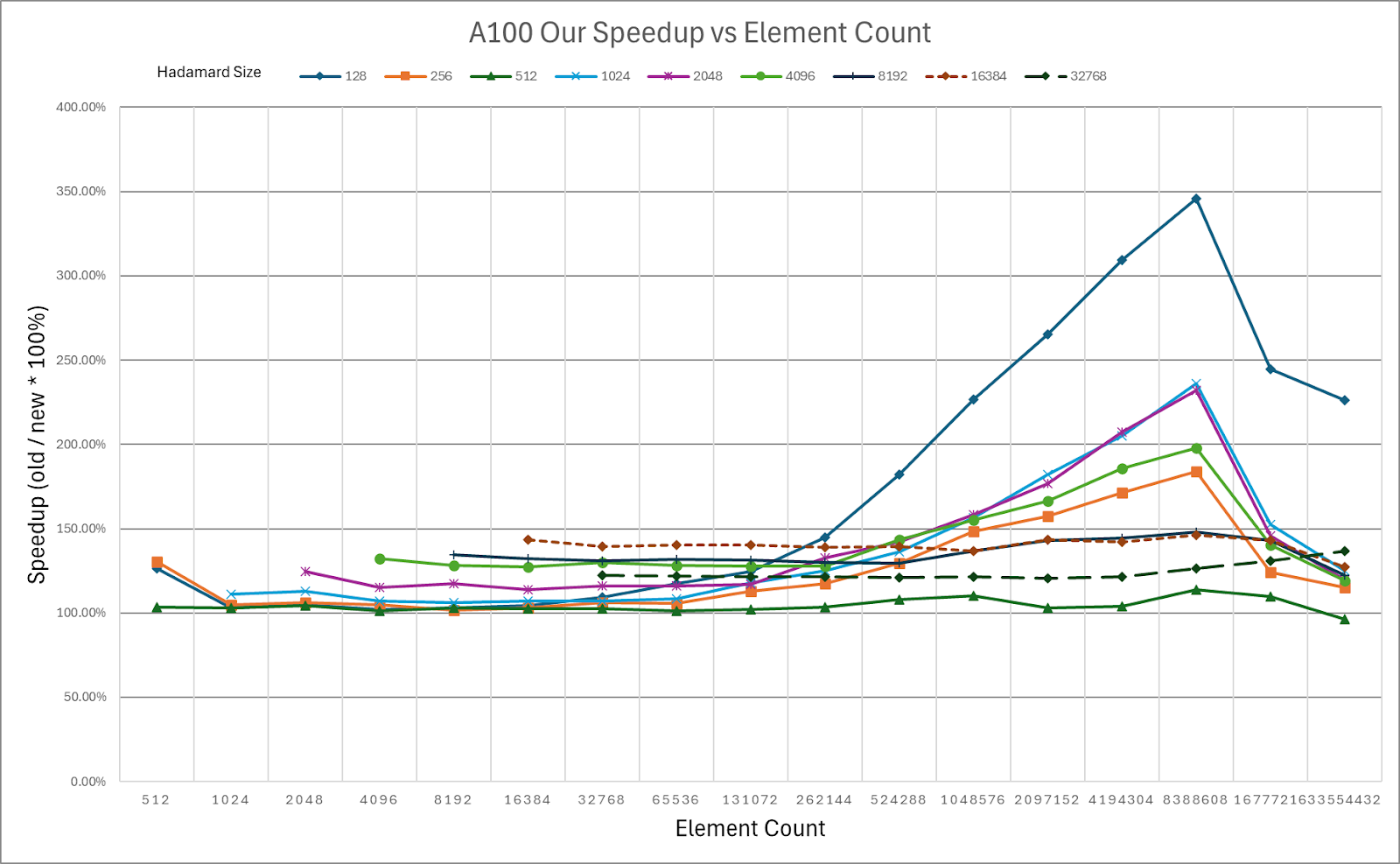
Figure 1: Speedup of HadaCore vs Dao AI Hadamard CUDA kernel. A peak gain of 3.46x on the A100 is achieved using 128 rotation by 8.4M elements.
The HadaCore Kernel is publicly available.
Background
QuaRot and SpinQuant both propose methods to increase the numerical accuracy of INT4 and INT8 quantization in LLMs. Both methods rotate model activations since rotations are statistically likely to reduce the magnitude of outliers, as it “distributes” extreme values among other (less extreme) dimensions, and rotation is also an easily invertible operation using the inverse of the rotation matrix. These methods can also improve FP8 inference accuracy, such as in FlashAttention-3.
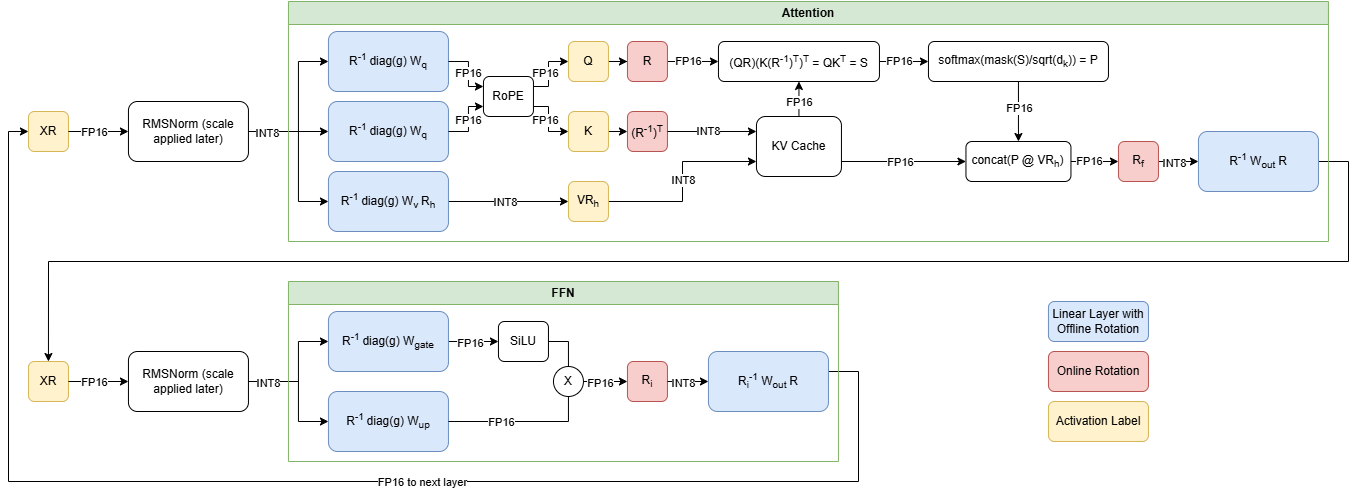
Figure 2. Transformer block showing online (red) and offline rotations (blue) in QuaRot
Applying these rotation matrices introduces model runtime overhead due to the online operations shown in Figure 2. These rotations can be applied through matrix multiplication, but the added overhead would diminish the benefits from quantization. Therefore, QuaRot and SpinQuant opt to use Walsh-Hadamard matrices, a special type of rotation matrix that can be applied faster than matrix multiplication using the Fast Walsh-Hadamard Transform algorithm. HadaCore is an optimized implementation of this algorithm for NVIDIA GPUs that support Tensor Cores.
Tensor Core Accelerated Hadamard Transform
HadaCore leverages NVIDIA Tensor Cores, which are specialized compute units on NVIDIA GPUs optimized for matrix multiplication. To achieve this, our kernel performs a hardware-aware work decomposition of the Fast Walsh-Hadamard algorithm. This work decomposition ensures that we can utilize the MMA PTX instructions that execute on the Tensor Core chip. HadaCore applies a 16×16 Hadamard transform to chunks of the input data. The computation can then be offloaded to the FP16 Tensor Core with usage of the mma.m16n8k16 instruction. The warp-level parallelism for HadaCore is shown below.

Figure 3: HadaCore Parallelization, 1×256 vectors (rows) being rotated by a size 256 Hadamard.
We process fragments of 256 elements in parallel using warp-level Tensor Core operations to achieve up to a 256-size Hadamard transform. For further sizes, we shuffle data between warps and repeat.
Microbenchmarks
We benchmark HadaCore against the Dao AI Lab Hadamard Kernel on both NVIDIA H100 and A100 GPUs across varying Hadamard and input tensor sizes.
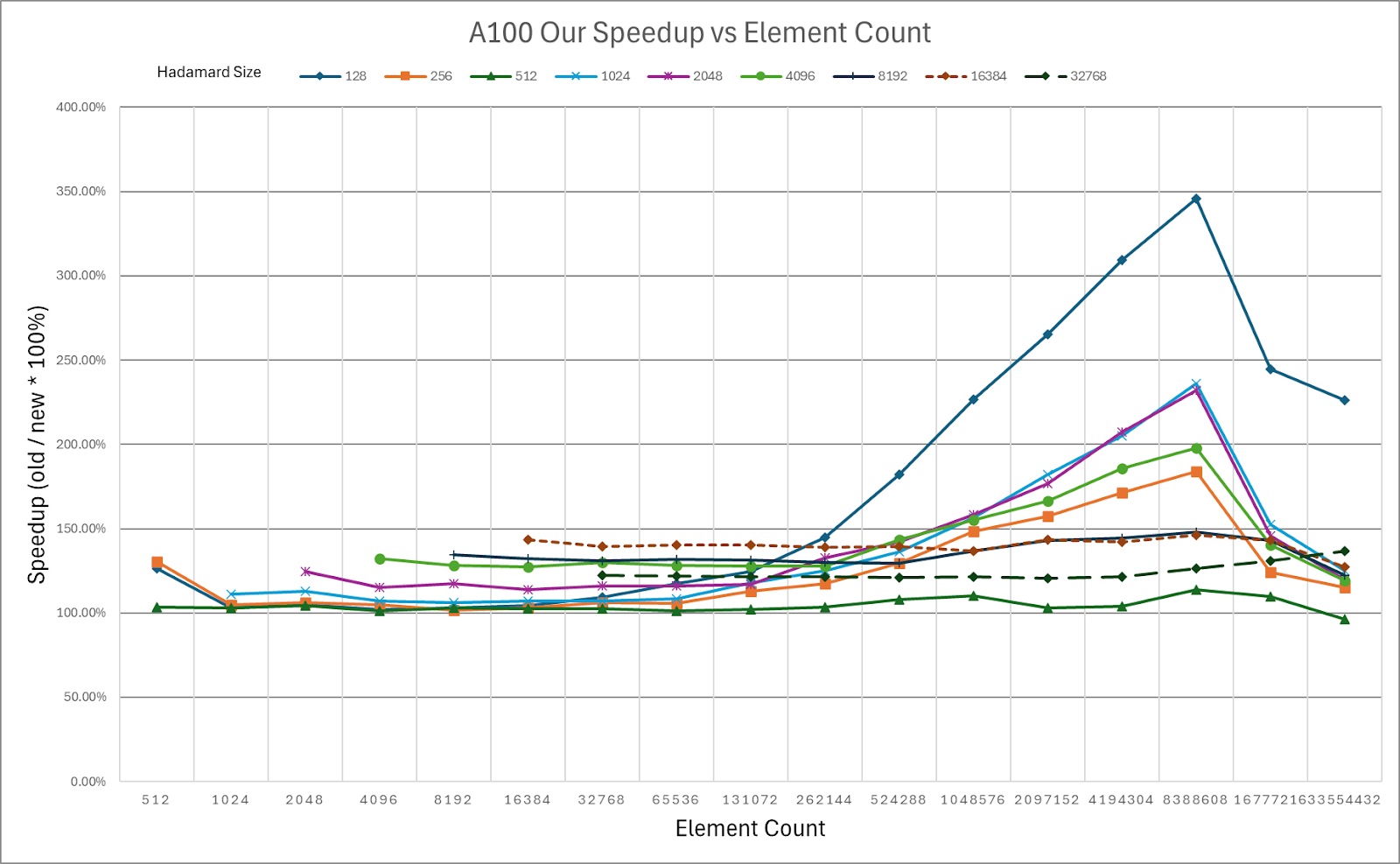
Figure 4: HadaCore Kernel Speedup on NVIDIA A100 over Dao AI Lab Fast Hadamard Kernel

Color coded Speedup Table for NVIDIA A100, Green = Speedup over Baseline
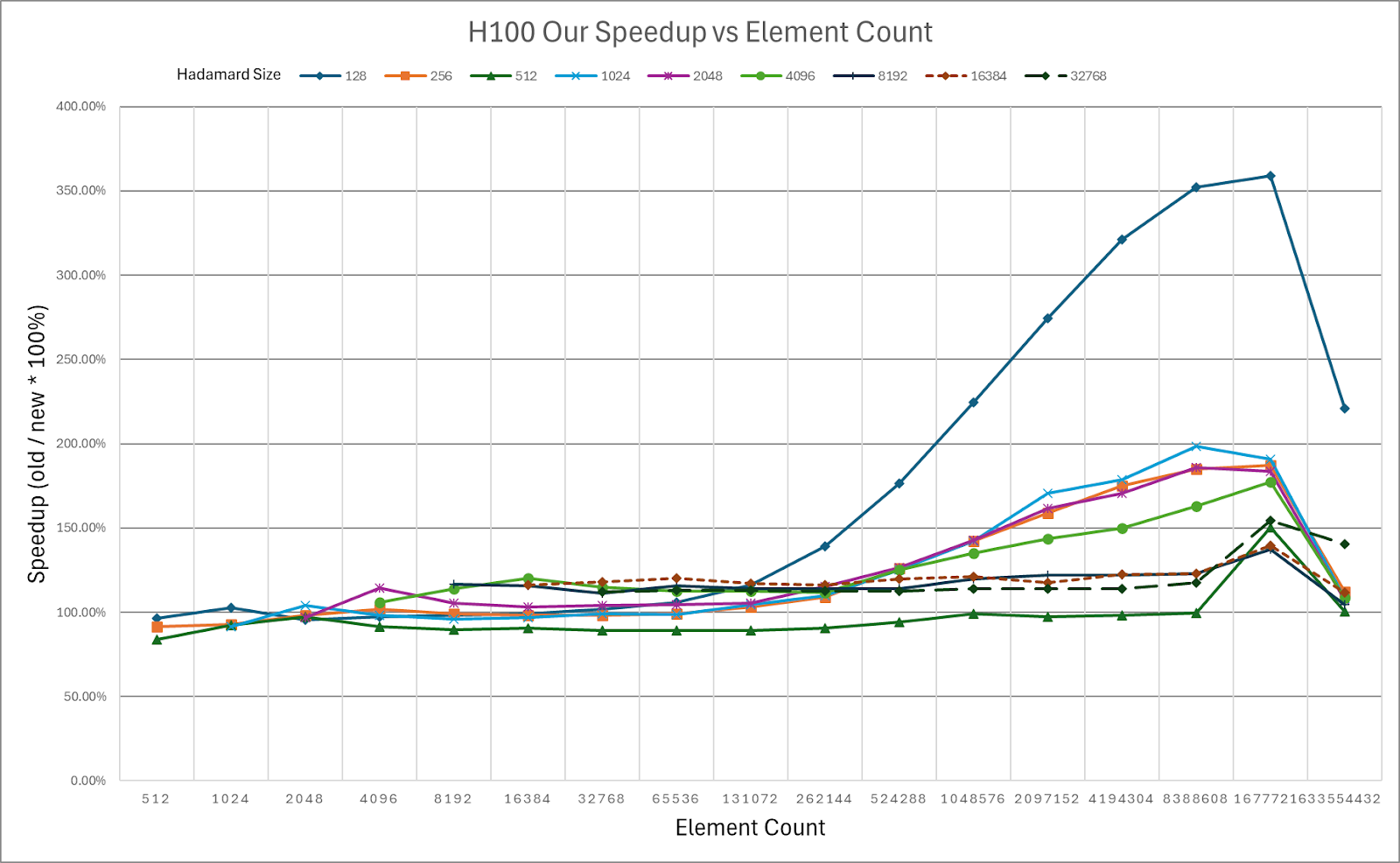
Figure 5: HadaCore Kernel Speedup on NVIDIA H100 over Dao AI Lab Fast Hadamard Kernel

Color coded Speedup Table for NVIDIA H100, Green = Speedup over Baseline
We showcase our speedup as the input tensor size (labeled element count) in our charts increase. Element count is the number of elements in the target matrix we are rotating. For example, in multi-head attention:
The queries (Q), keys (K) and values (V) tensors are 4D tensors of size:
(batch_size, seq_len, n_heads, head_dim)
A Hadamard matrix of size head_dim is applied to these activation tensors, so we refer to this as using a Hadamard size of head_dim with an element count of:
batch_size*seq_len*n_heads*head_dim.
Common element counts for query rotations in an attention block:
| Model \ Tokens | Prefill | Decoding |
| Llama-2 70b | 33,554,432 elements 128 Hadamard size (1 batch * 64 heads * 4096 tokens * 128 dimensional embeddings per head per token) |
8192 elements 128 Hadamard size (1 batch * 64 heads * 1 token * 128 dimensional embeddings per head per token) |
| Llama-3 8b | 33,554,432 elements 128 Hadamard size (1 batch * 32 heads * 8192 tokens * 128 dimensional embeddings per head per token) |
4,096 elements 128 Hadamard size (1 batch * 32 heads * 1 token * 128 dimensional embeddings per head per token) |
HadaCore achieves 1.1–1.4x speedup on A100 and 1.0–1.3x speedup on H100 over Dao AI Lab’s Fast Hadamard kernel, with a peak gain of 3.5x and 3.6x, respectively. For smaller sizes on H100, HadaCore’s gain decreases. For future work, we plan to incorporate usage of Hopper specific features like TMA and WGMMA for improved H100 performance.
MMLU Benchmarks
We evaluated MMLU scores on a Llama 3.1-8B inference workload where the FlashAttention computation was performed in FP8. Newer generation NVIDIA Hopper GPUs come equipped with FP8 Tensor Cores that deliver substantial compute gain over FP16.
Our results show the benefit of using HadaCore for accuracy preservation when combined with optimizations such as FP8 FlashAttention.
| Format | Method | Llama3.1-8B Avg. 5-Shot MMLU Accuracy |
| Q, K, V: FP16 FlashAttention: FP16 |
N/A | 65.38 |
| Q, K, V: FP16 FlashAttention: FP8 |
No Hadamard | 64.40 |
| Q, K, V: FP8 FlashAttention: FP8 |
HadaCore | 65.09 |
| Q, K, V: FP8 FlashAttention: FP8 |
Dao AI Fast Hadamard Kernel | 65.45 |
Table 1: MMLU scores for Llama3.1 8B with FP16 baseline and FP8 attention using Hadamard transforms, comparing an implementation with explicit Hadamard matrix multiplications vs. HadaCore (higher is better)
From the above MMLU scores, we note that for Llama3.1-8B inference with FP8 attention, HadaCore improves the quantization error introduced from computing attention in a lower precision.
Conclusion
We showcased our speedups achieved by moving the Fast-Walsh Hadamard algorithm into a CUDA kernel that leverages Tensor Core acceleration and achieves a peak speedup of 3.5x and 3.6x over the Dao AI Fast-Hadamard kernel on NVIDIA A100 and H100, respectively.
Further, we showed on the MMLU benchmark that rotating with HadaCore maintains similar quantization error reduction to the Fast-Hadamard kernel, while providing computational acceleration.
Future Work
We plan to implement a Triton version of our kernel and experiment with more advanced techniques such as kernel fusion to support fused Hadamard transform and quantization. Further, we plan to extend our kernel to support BF16 Tensor Core compute.